Wzór Debye'a (2.16) stanowi punkt wyjscia do prostego
matematycznego opisu dyfrakcji proszkowej. Dzieki niemu i informacjom
zawartym w poprzednich paragrafach (str.![[*]](/latex2html/icons/crossref.png) -
-![[*]](/latex2html/icons/crossref.png) ),
wyprowadzimy wzór na natezenie promieniowania rozproszonego w funkcji
wektora rozpraszania I(q) z uwzglednieniem skonczonych rozmiarów
rozpraszajacych krysztaów.
),
wyprowadzimy wzór na natezenie promieniowania rozproszonego w funkcji
wektora rozpraszania I(q) z uwzglednieniem skonczonych rozmiarów
rozpraszajacych krysztaów.
Poprzednio pokazano, ze wzór Debye'a mozna przepisac do postaci (2.21):
I(
q) =
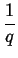
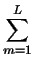
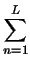 fmfn . FFT
fmfn . FFT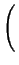
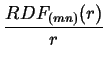 . SD
. SD(
r;
R)
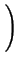
Definiuje on obserwowana krzywa dyfrakcyjna jako transformate furierowska
iloczynu dwóch funkcji: rozkadu radialnego struktury RDF(r)
podzielonego przez r i dystrybucji ksztatu krystalitu SD(r;R).
Na podstawie twierdzenia Stokesa (transformata iloczynu funkcji jest
splotem transformat tych funkcji okreslonym w przestrzeni odwrotnej)
mozna otrzymac:
I(q) = 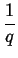 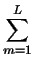 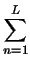 fmfn . fmfn . 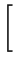 FFT FFT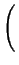 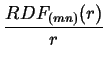 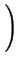 *FFT *FFT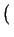 SD(r;R) SD(r;R)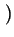 ![$\displaystyle \left.\vphantom{ FFT\left( \frac{RDF_{(mn)}(r)}{r}\right) *FFT\left( SD(r;R)\right) }\right]$](img218.png)
|
(2.24) |
W tej postaci wzór Debye'a jest splotem dwóch funkcji: transformaty
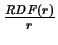 i transformaty dystrybucji ksztatu krystalitu
SD(r;R). Zarówno
i transformaty dystrybucji ksztatu krystalitu
SD(r;R). Zarówno
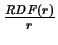 jak i SD(r;R)
sa funkcjami rzeczywistymi i interesujace sa tylko czesci cosinusowe
ich transformat. Rozwijajac pierwsza z transformat dostajemy:
jak i SD(r;R)
sa funkcjami rzeczywistymi i interesujace sa tylko czesci cosinusowe
ich transformat. Rozwijajac pierwsza z transformat dostajemy:
FFT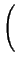 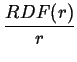 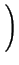 |
= |
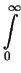 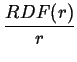 cos(q . r) dr = cos(q . r) dr = 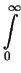 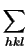 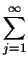 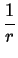 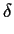 (r - jdhkl)cos(q . r) dr (r - jdhkl)cos(q . r) dr |
|
| |
= |
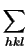 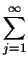 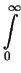 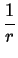 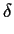 (r - jdhkl)cos(q . r) dr = (r - jdhkl)cos(q . r) dr = 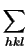 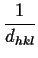 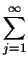 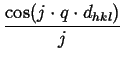 |
|
| |
|
|
(2.25) |
Szereg (2.25) jest rozbiezny o ile:
| q . dhkl |
= |
2n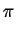 |
|
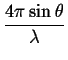 . dhkl . dhkl |
= |
2n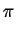 |
|
2dhklsin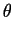 |
= |
n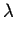 , , |
(2.26) |
czyli o ile speniony jest warunek Bragga. Jest on zas speniony dla
przeliczalnego zbioru wartosci wektora rozpraszania
q = qhkl = 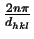 ,
wyznaczajacego poozenia refleksów bragowskich. Z kryterium cakowego
zbieznosci szeregów wiadomo, ze szereg typu
,
wyznaczajacego poozenia refleksów bragowskich. Z kryterium cakowego
zbieznosci szeregów wiadomo, ze szereg typu
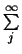
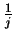 jest rozbiezny do +
jest rozbiezny do + 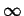 , wiec suma szeregu (2.25)
dla
q = qhkl =
, wiec suma szeregu (2.25)
dla
q = qhkl = 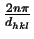 wynosi:
wynosi:
FFT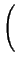 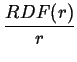 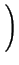 = = 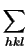 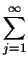 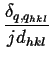 cos(j . q . dhkl) = cos(j . q . dhkl) = 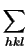 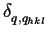 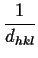 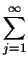 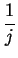 = = 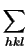 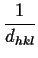 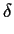 (q - qhkl) (q - qhkl)
|
(2.27) |
Dla wartosci wektora rozpraszania q niespeniajacych warunku
Bragga, suma szeregu (2.25) jest skonczona,
a wiec zaniedbywalna w porównaniu do (2.27).
Wynika stad, ze transformata
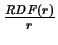 jest szeregiem
(``grzebieniem'') funkcji delta Diraca
jest szeregiem
(``grzebieniem'') funkcji delta Diraca
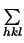
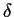 (q - qhkl)
zlokalizowanych w tych miejscach na dyfraktogramie, które odpowiadaja
poozeniom linii bragowskich, czyli wartosciom wektora rozpraszania
q = qhkl. Ów ``grzebien'' refleksów, spleciony na mocy
(2.24) z transformata dystrybucji ksztatu krystalitu
SD(r;R), czyli profilem linii dyfrakcyjnej, dajetypeset@protect
@@footnote
SF@gobble@opt
W przypadku ziaren niekulistych kazda rodzine refleksów hkl
splata sie z profilem linii wasciwym dla ksztatu ziarna w kierunku
rozpraszania.
pena krzywa rozpraszania (czyli dyfraktogram proszkowy).
(q - qhkl)
zlokalizowanych w tych miejscach na dyfraktogramie, które odpowiadaja
poozeniom linii bragowskich, czyli wartosciom wektora rozpraszania
q = qhkl. Ów ``grzebien'' refleksów, spleciony na mocy
(2.24) z transformata dystrybucji ksztatu krystalitu
SD(r;R), czyli profilem linii dyfrakcyjnej, dajetypeset@protect
@@footnote
SF@gobble@opt
W przypadku ziaren niekulistych kazda rodzine refleksów hkl
splata sie z profilem linii wasciwym dla ksztatu ziarna w kierunku
rozpraszania.
pena krzywa rozpraszania (czyli dyfraktogram proszkowy).
Poozenia linii mozna atwo obliczyc korzystajac ze wzoru Bragga,
dlatego zostana dalej pominiete. Istotnym natomiast jest stwierdzenie,
ze profil proszkowej linii dyfrakcyjnej jest transformata
furierowska dystrybucji ksztatu rozpraszajacego krystalitutypeset@protect
@@footnote
SF@gobble@opt
Jak powiedziano w paragrafie 2.1.3, dystrybucja
ksztatu SD(r;R) jest parzysta funkcja r, dlatego profil
linii dyfrakcyjnej jest transformata cosinusów dystrybucji
ksztatu.
(por. [41] i [42]).
Korzystajac z tego twierdzenia wyprowadzimy w nastepnych paragrafach
wzory na profil linii dyfrakcyjnej szczególnie waznych rodzajów krysztaów:
- krysztaów w formie graniastosupa
- krysztaów kulistych lub o ksztatach bliskich kuli: izotropowych
oraz nieregularnych
- krysztaów kulistych z rozkadem wielkosci ziaren
Wyprowadzone wyrazenia sprawdzimy otrzymujac na ich podstawie równanie
Scherrera, wyznaczajac staa Scherrera i upewniajac sie, ze speniaja
prawo Poroda. Przedstawimy tez prosta metode okreslania penego rozkadu
wielkosci ziaren na podstawie pomiaru dwóch szerokosci linii dyfrakcyjnej:
na
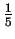 i
i
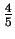 jej wysokosci.
jej wysokosci.
Subsections
roman pielaszek
2003-01-13
![]() -
-![]() ),
wyprowadzimy wzór na natezenie promieniowania rozproszonego w funkcji
wektora rozpraszania I(q) z uwzglednieniem skonczonych rozmiarów
rozpraszajacych krysztaów.
),
wyprowadzimy wzór na natezenie promieniowania rozproszonego w funkcji
wektora rozpraszania I(q) z uwzglednieniem skonczonych rozmiarów
rozpraszajacych krysztaów.
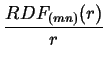 . SD(r;R)
. SD(r;R)