W paragrafie 2.3.3 podano wyrazenie (2.32)
na profil linii dyfrakcyjnej pochodzacej od proszku zozonego z kulistych
krysztaów majacych ten sam rozmiar R. W praktyce doswiadczalnej
mamy jednak do czynienia z proszkami stanowiacymi mieszanine ziaren
o niejednakowych rozmiarach. W takim przypadku do opisu wielkosci
ziarna nie wystarczy pojedynczy parametr R; nalezy uzyc rozkadu
wielkosci ziaren, danego co najmniej dwoma wielkosciami: srednim
wymiarem ziarna < R > i dyspersja 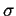 . Aby otrzymac
profil linii dyfrakcyjnej pochodzacej od takiego proszku nalezy scakowac
wyrazenie (2.32) na profil linii z zadanym rozkadem
wielkosci ziaren (GSD):
. Aby otrzymac
profil linii dyfrakcyjnej pochodzacej od takiego proszku nalezy scakowac
wyrazenie (2.32) na profil linii z zadanym rozkadem
wielkosci ziaren (GSD):
LPGSD(q; < R > ,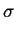 ) = ) = 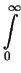 GSD(r, R) . GSD(r, R) . 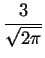 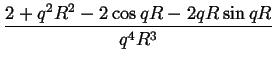 dR dR
|
(2.40) |
Postac samej funkcji rozkadu wielkosci ziaren podyktowana jest zazwyczaj
mechanizmem syntezy proszku. Najczestszym wyborem jest log-normalny
rozkad wielkosci ziaren (uzylismy go poprzednio wyliczajac dyfraktogramy
ab initio). Niestety, wyrazenie (2.40) jest
niecakowalne analitycznie dla szerokiej klasy asymetrycznych krzywych
dzwonowych w tym równiez dla rozkadu log-normalnego. Caka (2.40)
istnieje jednak w postaci analitycznej dla potegowo-wykadniczego
rozkadu wielkosci ziaren:
GSD(R;R0, m) 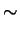 Rme-R/R0, Rme-R/R0,
|
(2.41) |
gdzie R0 i m sa parametrami definiujacymi ksztat
rozkadutypeset@protect
@@footnote
SF@gobble@opt
Funkcje uzywane jako rozkady wielkosci ziaren maja najprostsza postac
w ``swoich wasnych'' zmiennych. Np. rozkad log-normalny tradycyjnie
definiuje sie przez podanie mediany Ro i dyspersji
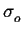 zmiennej log(R), zas rozkad potegowo-wykadniczy - zmiennymi
m i R0. Natywne zmienne tych rozkadów nie maja ze
soba zwiazku, natomiast wartosc oczekiwana < R > i dyspersja
zmiennej log(R), zas rozkad potegowo-wykadniczy - zmiennymi
m i R0. Natywne zmienne tych rozkadów nie maja ze
soba zwiazku, natomiast wartosc oczekiwana < R > i dyspersja
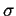 sa dla kazdego rozkadu zdefiniowane identycznie i
mozna je porównywac.
, których interpretacje podamy w dalszej czesci. Rozkad wykadniczo
potegowy (rys. 2.23) jest analogiczny do rozkadu
Poissona, jednak zmienna m ma tu charakter ciagy. Z punktu
widzenia zastosowan praktycznych jest on tez na tyle podobny do rozkadu
log-normalnego, ze moze byc traktowany jako jego zamiennik (pokazano
to w dalszej czesci pracy, patrz rys. 2.28).
sa dla kazdego rozkadu zdefiniowane identycznie i
mozna je porównywac.
, których interpretacje podamy w dalszej czesci. Rozkad wykadniczo
potegowy (rys. 2.23) jest analogiczny do rozkadu
Poissona, jednak zmienna m ma tu charakter ciagy. Z punktu
widzenia zastosowan praktycznych jest on tez na tyle podobny do rozkadu
log-normalnego, ze moze byc traktowany jako jego zamiennik (pokazano
to w dalszej czesci pracy, patrz rys. 2.28).
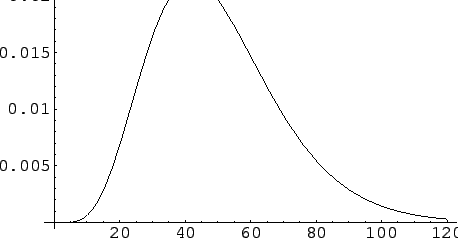
Figure:
Rozkad wielkosci ziaren (2.43)
typu
Rme-R/R0 wykreslony dla parametrów
R0 = 8,
m = 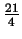 .
Srednia wielkosc ziarna wynosi w tym przypadku
< R > = 50Å,
zas dyspersja
.
Srednia wielkosc ziarna wynosi w tym przypadku
< R > = 50Å,
zas dyspersja
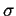 = 20Å.
= 20Å.
|
|
Odwrotnosc caki (staa normujaca) rozkadu (2.41)
wynosi:
A = 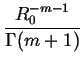 , ,
|
(2.42) |
gdzie 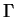 jest funkcja gamma Eulera. Unormowany rozkad
(2.41) jest wiec postaci:
jest funkcja gamma Eulera. Unormowany rozkad
(2.41) jest wiec postaci:
GSD(R;R0, m) = 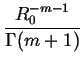 Rme-R/R0 Rme-R/R0
|
(2.43) |
Srednia wielkosc ziarna (moment rzedu 1) powyzszego rozkadu wynosi:
< R > = 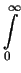 GSD(R;R0, m)R dR = GSD(R;R0, m)R dR = 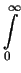 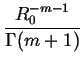 Rme-R/R0R dR = (m + 1)R0, Rme-R/R0R dR = (m + 1)R0,
|
(2.44) |
moment drugiego rzedu:
< R2 > = 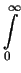 GSD(R;R0, m)R2dR = GSD(R;R0, m)R2dR = 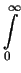 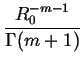 Rme-R/R0R2 dR = (m + 1)(m + 2)R02, Rme-R/R0R2 dR = (m + 1)(m + 2)R02,
|
(2.45) |
zas dyspersja:
Parametry R0 i m rozkadu (2.41)
powiazane sa z jego wartoscia oczekiwana i dyspersja w nastepujacy
sposób:
| R0 |
= |
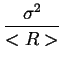 |
(2.47) |
| m |
= |
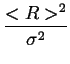 - 1 - 1 |
(2.48) |
Parametr m (a dokadnie: m + 1) moze byc traktowany jako
miara wzglednej szerokosci rozkadu (2.43).
Duza wartosc m oznacza rozkad waski zas maa - szeroki.
Ostatnie dwa wyrazenia pozwalaja na przepisanie rozkadu (2.43)
z uzyciem parametrów < R > i 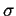 posiadajacych bezposrednia
interpretacje fizyczna zamiast R0 i m:
posiadajacych bezposrednia
interpretacje fizyczna zamiast R0 i m:
GSD(R; < R > ,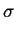 ) = ) = 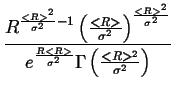 , ,
|
(2.49) |
gdzie < R > jest srednia wazona rozkadu, czyli srednia wielkoscia
ziarna w proszku wyrazona w Å. 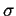 jest dyspersja
rozmiarów ziaren, czyli szerokoscia rozkadu, równiez wyrazona w Å.
Rozkad wielkosci ziaren dany przez (2.49) przypomina
ksztatem rozkad log-normalny i moze byc z powodzeniem traktowany
jako jego funkcjonalny odpowiednik. Maksimum rozkadu (2.49)
znajduje sie w:
jest dyspersja
rozmiarów ziaren, czyli szerokoscia rozkadu, równiez wyrazona w Å.
Rozkad wielkosci ziaren dany przez (2.49) przypomina
ksztatem rozkad log-normalny i moze byc z powodzeniem traktowany
jako jego funkcjonalny odpowiednik. Maksimum rozkadu (2.49)
znajduje sie w:
Rmax = < R > - 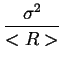 , ,
|
(2.50) |
czyli najliczniej wystepujace ziarna maja srednice nieco mniejsza
niz srednia wielkosc ziarna w proszku.
Wyrazenie (2.40) na profil linii dyfrakcyjnej dla
proszku z niezerowa dyspersja wielkosci ziaren wyrazimy dla prostoty
najpierw w zmiennych R0 i m, podstawiajac (2.43):
LPGSD(q;R0, m) = 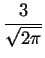 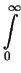 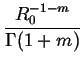 Rme-R/R0 . Rme-R/R0 . 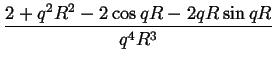 dR dR
|
(2.51) |
Caka (2.51) istnieje o ile wielkosci q,
(m + 1) oraz R0 sa rzeczywiste i dodatnie, co jest
spenione ze wzgledu na ich sens fizyczny. Po wykonaniu cakowania
otrzymujemy:
| LPGSD(q;R0, m) |
= |
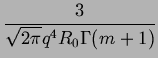 . . |
|
| |
|
![$\displaystyle \left\{\vphantom{ \frac{2\Gamma (m-2)}{R_{0}^{2}}-\frac{2\left( 1...
...c{m}{2}}\cos \left[ (m-2)\arctan qR_{0}\right] \Gamma (m-2)}{R_{0}^{2}}}\right.$](img297.png) 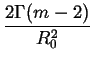 - - ![$\displaystyle {\frac{{2\left( 1+q^{2}R_{0}^{2}\right) ^{1-\frac{m}{2}}\cos \left[ (m-2)\arctan qR_{0}\right] \Gamma (m-2)}}{{R_{0}^{2}}}}$](img299.png) |
|
| |
|
+ ![$\displaystyle \left.\vphantom{ q^{2}\Gamma (m)-\frac{2q\left( 1+q^{2}R_{0}^{2}\...
...-m)}{2}}\sin \left[ (m-1)\arctan qR_{0}\right] \Gamma (m-1)}{R_{0}^{2}}}\right.$](img300.png) q2 q2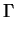 (m) - (m) - ![$\displaystyle {\frac{{2q\left( 1+q^{2}R_{0}^{2}\right) ^{\frac{(1-m)}{2}}\sin \left[ (m-1)\arctan qR_{0}\right] \Gamma (m-1)}}{{R_{0}^{2}}}}$](img302.png) ![$\displaystyle \left.\vphantom{ q^{2}\Gamma (m)-\frac{2q\left( 1+q^{2}R_{0}^{2}\...
...m)}{2}}\sin \left[ (m-1)\arctan qR_{0}\right] \Gamma (m-1)}{R_{0}^{2}}}\right\}$](img303.png) . . |
|
| |
|
|
(2.52) |
W powyzszym wzorze funkcje gamma Eulera wystepuja w liczniku i mianowniku,
dlatego mozna je uproscic.
Ponizej podajemy najprostsza scisa postac wyrazenia na profil
linii dyfrakcyjnej proszku zozonego z kulistych ziaren z wykadniczo-potegowym
rozkadem wielkosci:
| LPGSD(q;R0, m) |
= |
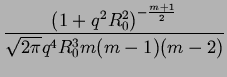 . . |
|
| |
|
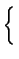 3 3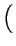 1 + q2R02 1 + q2R02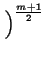 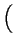 2 + q2R02(m - 1)(m - 2) 2 + q2R02(m - 1)(m - 2)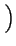 |
|
| |
|
-6 1 + q2R02 1 + q2R02 cos cos (m - 2)arctan qR0 (m - 2)arctan qR0![$\displaystyle \left.\vphantom{ (m-2)\arctan qR_{0}}\right]$](img312.png) |
(2.53) |
| |
|
- ![$\displaystyle \left.\vphantom{ 6qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right.$](img313.png) 6qR0 6qR0 1 + q2R02 1 + q2R02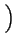 (m - 2)sin (m - 2)sin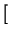 (m - 1)arctan qR0 (m - 1)arctan qR0![$\displaystyle \left.\vphantom{ (m-1)\arctan qR_{0}}\right]$](img316.png) ![$\displaystyle \left.\vphantom{ 6qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right\}$](img317.png) . . |
|
Wyrazenie (2.53) skada sie wyacznie z funkcji
elementarnych i moze byc wygodnie uzywane zarówno w obliczeniach numerycznych
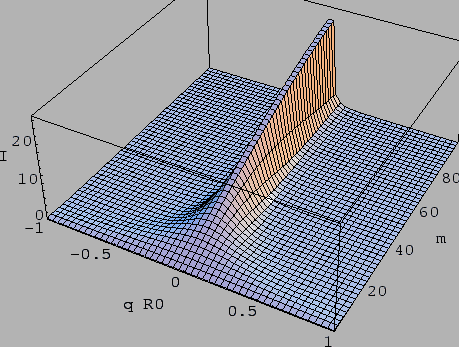
jak i do dalszych przeksztacen symbolicznych. Rysunek (2.24)
pokazuje silna zaleznosc profilu linii dyfrakcyjnej od parametru m
(bedacego miara wzglednej szerokosci rozkadu wielkosci ziaren).
Natezenie linii w jej maksimum (q = 0) mozna obliczyc przechodzac
w (2.53) do granicy
q 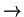 0:
0:
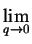 LPGSD(q;R0, m) = LPGSD(q;R0, m) = 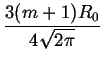
|
(2.54) |
Podstawienie do (2.53) zaleznosci (2.47)
i (2.48) oraz wykonanie prostych przeksztacen pozwala
przejsc od parametrów rozkadu wykadniczo-potegowego (R0, m)
do parametrów statystycznych (
< R > ,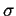 ).
).
Otrzymujemy wyrazenie na profil linii dyfrakcyjnej proszku
polidyspersyjnego jako funkcje < R > i 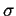 , majacych
bezposrednia fizyczna interpretacje:
, majacych
bezposrednia fizyczna interpretacje:
LPGSD(q; < R > ,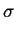 ) = ) = 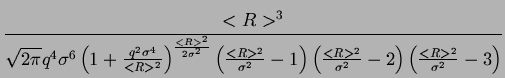 . . |
|
|
|
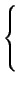 3 3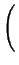 1 + 1 + 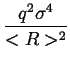 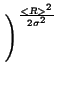 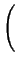 2 + 2 + 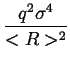 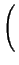 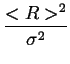 - 2 - 2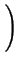 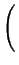 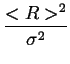 - 3 - 3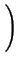 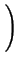 |
|
|
|
-6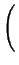 1 + 1 + 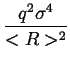 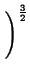 cos cos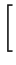 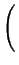 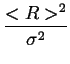 - 3 - 3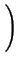 arctan arctan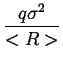 ![$\displaystyle \left.\vphantom{ \left( \frac{<R>^{2}}{\sigma ^{2}}-3\right) \arctan \frac{q\sigma ^{2}}{<R>}}\right]$](img337.png) |
|
|
|
- ![$\displaystyle \left.\vphantom{ 6\frac{q\sigma ^{2}}{<R>}\left( 1+\frac{q^{2}\si...
...<R>^{2}}{\sigma ^{2}}-2\right) \arctan \frac{q\sigma ^{2}}{<R>}\right] }\right.$](img338.png) 6 6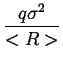 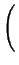 1 + 1 + 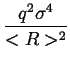 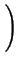 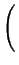 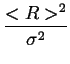 - 3 - 3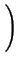 sin sin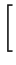 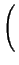 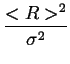 - 2 - 2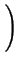 arctan arctan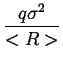 ![$\displaystyle \left.\vphantom{ \left( \frac{<R>^{2}}{\sigma ^{2}}-2\right) \arctan \frac{q\sigma ^{2}}{<R>}}\right]$](img341.png) ![$\displaystyle \left.\vphantom{ 6\frac{q\sigma ^{2}}{<R>}\left( 1+\frac{q^{2}\si...
...R>^{2}}{\sigma ^{2}}-2\right) \arctan \frac{q\sigma ^{2}}{<R>}\right] }\right\}$](img342.png) . . |
|
|
|
| |
|
|
(2.55) |
Wyrazenie powyzsze, bedac dokadnym odpowiednikiem (2.53),
jest uzyteczne jako scisy wzór na profil linii dyfrakcyjnej proszku
z rozkadem wielkosci ziaren wyrazony w zrozumiaych jednostkach,
ale jest od (2.53) duzsze i bardziej zagmatwane.
Dlatego do dalszych przeksztacen algebraicznych wykorzystywac bedziemy
raczej (2.53) niz (2.55) pamietajac
o ich wzajemnej równowaznosci. Wyrazenie (2.55)
na proszkowa linie dyfrakcyjna z rozkadem wielkosci ziaren jest uogólnieniem
wzoru (2.32) na linie dyfrakcyjna pojedynczego krystalitu
i w szczególnym przypadku zerowej dyspersji powinno sie do niego upraszczac.
Istotnie, przechodzac w (2.55) z dyspersja do granicy
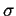
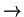 0, dostajemy:
0, dostajemy:
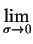 LPGSD(q; < R > , LPGSD(q; < R > ,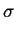 ) = ) = 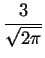 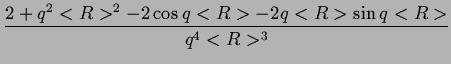 , ,
|
(2.56) |
czyli wyrazenie monodyspersyjne.
roman pielaszek
2003-01-13
![]() . Aby otrzymac
profil linii dyfrakcyjnej pochodzacej od takiego proszku nalezy scakowac
wyrazenie (2.32) na profil linii z zadanym rozkadem
wielkosci ziaren (GSD):
. Aby otrzymac
profil linii dyfrakcyjnej pochodzacej od takiego proszku nalezy scakowac
wyrazenie (2.32) na profil linii z zadanym rozkadem
wielkosci ziaren (GSD):

![]() posiadajacych bezposrednia
interpretacje fizyczna zamiast R0 i m:
posiadajacych bezposrednia
interpretacje fizyczna zamiast R0 i m:
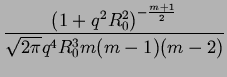 .
. 
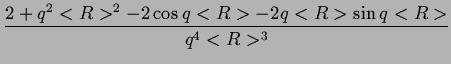 ,
,