Wielkosc nazywana szerokoscia poówkowa linii dyfrakcyjnej, FWHM
(Full Width at Half Maximum), jest bardzo chetnie stosowanym
w krystalografii parametrem, gównie za sprawa atwosci jej pomiaru.
W przypadku krystalicznych proszków skadajacych sie w ziaren o identycznych
wielkosciach istnieje prosta zaleznosc pomiedzy szerokoscia poówkowa
a wielkoscia krystalitu, nazywana równaniem Scherrera, co opisano
w paragrafach 2.3.2 i 2.3.4.
W bardziej realistycznym przypadku proszków z rozrzutem wielkosci
ziaren pojedynczy parametr jakim jest FWHM nie wystarczy do
ustalenia obu parametrów rozkadu: jego wartosci sredniejtypeset@protect
@@footnote
SF@gobble@opt
Jak pokazano w paragrafie 2.3.7 FWHM
nie wystarczy do dokadnego ustalenia nawet samej wartosci sredniej,
bowiem równanie Scherrera zawodzi dla proszków z rozrzutem wielkosci
ziarna.
i dyspersji. Do znalezienia tych dwóch niewiadomych potrzebne sa
dwa równania - dlatego do wyznaczenia rozkadu wielkosci ziaren uzyjemy
nie jednej a dwóch szerokosci linii: w
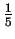 i
i
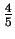 jej wysokosci (czyli
FW
jej wysokosci (czyli
FW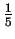 M i
FW
M i
FW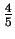 M).
Teoretycznie najlepiej mierzyc szerokosci linii tam gdzie róznia sie
najbardziej, czyli blisko wierzchoka i u podstawy linii. Z praktyki
natomiast wiadomo, ze niewiele punktów doswiadczalnych wierzchoka
i problemy z odcieciem ta u podstawy moga powodowac duze bedy pomiarowe
szerokosci linii. Uzyte wartosci
M).
Teoretycznie najlepiej mierzyc szerokosci linii tam gdzie róznia sie
najbardziej, czyli blisko wierzchoka i u podstawy linii. Z praktyki
natomiast wiadomo, ze niewiele punktów doswiadczalnych wierzchoka
i problemy z odcieciem ta u podstawy moga powodowac duze bedy pomiarowe
szerokosci linii. Uzyte wartosci
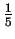 i
i
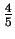 stanowia kompromis miedzy teoria a praktyka. Stwierdzono, ze sa one
uzyteczne zarówno dla dyfraktogramów wyliczonych numerycznie jak i
zmierzonych doswiadczalnie.
stanowia kompromis miedzy teoria a praktyka. Stwierdzono, ze sa one
uzyteczne zarówno dla dyfraktogramów wyliczonych numerycznie jak i
zmierzonych doswiadczalnie.
Podobnie jak w poprzednim paragrafie, wykorzystamy wyrazenie (2.53)
na profil linii dyfrakcyjnej proszku z rozkadem wielkosci ziaren
w zmiennych R0 i m. Potrzebujemy otrzymac dwa równania
na szerokosci linii: mierzone na
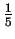 oraz
oraz
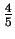 wysokosci jej maksimum. Jest to praca identyczna do wykonanej poprzednio,
kiedy otrzymalismy wyrazenie na szerokosc linii w poowie jej wysokosci
(równanie Scherrera). Uzylismy wtedy wspóczynnika h, który
wyraza uamek wysokosci linii i wynosi
wysokosci jej maksimum. Jest to praca identyczna do wykonanej poprzednio,
kiedy otrzymalismy wyrazenie na szerokosc linii w poowie jej wysokosci
(równanie Scherrera). Uzylismy wtedy wspóczynnika h, który
wyraza uamek wysokosci linii i wynosi
 . Tym razem
poozymy najpierw
h =
. Tym razem
poozymy najpierw
h = 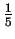 a potem
h =
a potem
h = 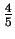 ,
zachowujac wyprowadzenie od (2.57)
do (2.61) bez zadnej zmiany. Numeryczne
rozwiazanie równan (2.61) daje dwie
krzywe x(m) o nieznanej postaci analitycznej, które jednak
mozemy przyblizyc funkcjami cotangens otrzymujac:
,
zachowujac wyprowadzenie od (2.57)
do (2.61) bez zadnej zmiany. Numeryczne
rozwiazanie równan (2.61) daje dwie
krzywe x(m) o nieznanej postaci analitycznej, które jednak
mozemy przyblizyc funkcjami cotangens otrzymujac:
| xh=1/5(m) |
 |
-0.0081 + 0.0208 . ctg(0.004238 + 0.003675 . m) |
(2.70) |
| xh=4/5(m) |
 |
0.001555 + 0.00884 . ctg(0.00972 + 0.00453 . m) |
(2.71) |
Powyzsze krzywe x(m), stanowiace rozwiazania równania (2.61)
i ich dopasowania funkcja ctg pokazano, odpowiednio, na rys. 2.27 a i b.
Figure:
Numeryczne rozwiazania równania
przestepnego (2.61) na szerokosc profilu
linii dyfrakcyjnej mierzona na wysokosci (a)
h = 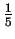 oraz (b)
h =
oraz (b)
h = 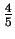 maksimum tej linii.
Ciagi rozwiazan wyznaczaja zaleznosc
x(m) (punkty
na wykresach), która mozna przyblizyc funkcja typu
x(m) = A + B . ctg(C + D . m)
- (linie ciage).
maksimum tej linii.
Ciagi rozwiazan wyznaczaja zaleznosc
x(m) (punkty
na wykresach), która mozna przyblizyc funkcja typu
x(m) = A + B . ctg(C + D . m)
- (linie ciage).
|
a)
 |
b)
 |
|
Pamietajac, ze podstawilismy x = qR0, znajac rozwiazania
x1/5(m)
i
x4/5(m) w postaci funkcji (2.70) i (2.71)
oraz dysponujac zmierzonymi szerokosciami linii
FW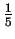 M
i
FW
M
i
FW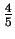 M, mozemy zapisac ukad równan:
którego dwie niewiadome R0 i m mozna atwo obliczyc
metoda podstawiania. Nastepnie, korzystajac z tozsamosci (2.47)
i (2.48), mozna przejsc ze zmiennych (R0, m)
do
( < R > ,
M, mozemy zapisac ukad równan:
którego dwie niewiadome R0 i m mozna atwo obliczyc
metoda podstawiania. Nastepnie, korzystajac z tozsamosci (2.47)
i (2.48), mozna przejsc ze zmiennych (R0, m)
do
( < R > ,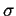 ).
).
Wzorytypeset@protect
@@footnote
SF@gobble@opt
Przypomnienie: w czesci teoretycznej na dyfraktogramach operujemy
wyacznie w jednostkach wektora rozpraszania
q =  .
Szerokosci linii dyfrakcyjnych
FW
.
Szerokosci linii dyfrakcyjnych
FW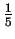 M i
FW
M i
FW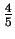 M
wyrazone sa wiec w q, czyli Å-1. Odpowiednio,
wielkosci zwiazane z rozmiarami w przestrzeni prostej (np. < R >
i
M
wyrazone sa wiec w q, czyli Å-1. Odpowiednio,
wielkosci zwiazane z rozmiarami w przestrzeni prostej (np. < R >
i 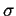 ) sa wyrazone w Å.
na sredni rozmiar ziarna w proszku i dyspersje GSD
jako funkcje mierzalnych wielkosci
FW
) sa wyrazone w Å.
na sredni rozmiar ziarna w proszku i dyspersje GSD
jako funkcje mierzalnych wielkosci
FW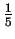 M i
FW
M i
FW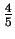 M
proszkowej lini dyfrakcyjnej maja postac:
M
proszkowej lini dyfrakcyjnej maja postac:
gdzie pomocnicze wspóczynniki A, B i C wynosza:
| A |
= |
arcctg 277069 - 105723 277069 - 105723  |
|
| B |
= |
0.001555 + 0.00884 . ctg 0.002237 - 2101 . A 0.002237 - 2101 . A |
|
| C |
= |
-0.6515 - 463695 . A |
|
Na rys. 2.28 przedstawiono przykady
oznaczen rozkadu wielkosci ziaren zaproponowana metoda dla dyfraktogramów
proszkowych wyliczonych teoretycznie (ab initio). Przedstawione
dyfraktogramy zostay otrzymane metodami opisanymi w paragrafie 2.2.3
przy uzyciu log-normalnego rozkadu wielkosci ziaren. Na tak otrzymanym
dyfraktogramie dokonano pomiaru szerokosci linii (111) oraz
(113) na
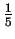 i
i
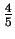 wysokosci,
uzyto wzorów (2.73) otrzymujac parametry
< R > i
wysokosci,
uzyto wzorów (2.73) otrzymujac parametry
< R > i 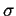 . Nastepnie wykreslono na ich podstawie
rozkad wielkosci ziaren (2.49), widoczny po prawej
stronie rys. 2.28 (czerwona
krzywa) razem z log-normalnym rozkadem wielkosci ziaren uzytym podczas
obliczania profili dyfrakcyjnych (czarna, urwanatypeset@protect
@@footnote
SF@gobble@opt
Jak powiedziano w paragrafie 2.2.3, maksymalny
rozmiar ziarna przy obliczaniu profili dyfrakcyjnych proszków metoda
'ab initio' podlega ograniczeniom. Dlatego otrzymany rozkad
wielkosci ziaren poczatkowo ma postac log-normalna lecz po przekroczeniu
zadanego limitu rozmiaru, dalsze obliczenia sa zaniedbywane. Oznacza
to, ze powyzej tego limitu rozkad urywa sie (jest zawsze zero).
krzywa). Z rys. 2.28 widac
wyraznie, ze uzyty w proponowanej metodzie wykadniczo-potegowy rozkad
wielkosci ziaren, chociaz istotnie rózni sie w sensie matematycznym
od rozkadu log-normalnego, dobrze oddaje jego charaktertypeset@protect
@@footnote
SF@gobble@opt
Najwieksza zaleta rozkadu wykadniczo-potegowego, jest to, ze istnieje
analityczna postac caki profilu proszkowej linii dyfrakcyjnej (2.51),
a dzieki temu - opisywana metoda wyznaczania rozkadu wielkosci ziaren.
. W praktycznych zastosowaniach jest on z pewnoscia wystarczajacy.
Trzeba natomiast powiedziec, ze kazda ilosciowa analiza profilu linii
dyfrakcyjnej, waczajac w to opisywana metode
FW
. Nastepnie wykreslono na ich podstawie
rozkad wielkosci ziaren (2.49), widoczny po prawej
stronie rys. 2.28 (czerwona
krzywa) razem z log-normalnym rozkadem wielkosci ziaren uzytym podczas
obliczania profili dyfrakcyjnych (czarna, urwanatypeset@protect
@@footnote
SF@gobble@opt
Jak powiedziano w paragrafie 2.2.3, maksymalny
rozmiar ziarna przy obliczaniu profili dyfrakcyjnych proszków metoda
'ab initio' podlega ograniczeniom. Dlatego otrzymany rozkad
wielkosci ziaren poczatkowo ma postac log-normalna lecz po przekroczeniu
zadanego limitu rozmiaru, dalsze obliczenia sa zaniedbywane. Oznacza
to, ze powyzej tego limitu rozkad urywa sie (jest zawsze zero).
krzywa). Z rys. 2.28 widac
wyraznie, ze uzyty w proponowanej metodzie wykadniczo-potegowy rozkad
wielkosci ziaren, chociaz istotnie rózni sie w sensie matematycznym
od rozkadu log-normalnego, dobrze oddaje jego charaktertypeset@protect
@@footnote
SF@gobble@opt
Najwieksza zaleta rozkadu wykadniczo-potegowego, jest to, ze istnieje
analityczna postac caki profilu proszkowej linii dyfrakcyjnej (2.51),
a dzieki temu - opisywana metoda wyznaczania rozkadu wielkosci ziaren.
. W praktycznych zastosowaniach jest on z pewnoscia wystarczajacy.
Trzeba natomiast powiedziec, ze kazda ilosciowa analiza profilu linii
dyfrakcyjnej, waczajac w to opisywana metode
FW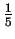 /
/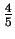 M,
jest wrazliwa na wszelkie znieksztacenia linii, np. pochodzace od
bedów uozenia czy naprezen sieci krystalicznej, co szerzej omówiono
w ``Uwagach praktycznych'' dodatku A.1.
M,
jest wrazliwa na wszelkie znieksztacenia linii, np. pochodzace od
bedów uozenia czy naprezen sieci krystalicznej, co szerzej omówiono
w ``Uwagach praktycznych'' dodatku A.1.
Przedstawione na rys. 2.28 porównanie
jest - jak sie wydaje - jedyna dostepna forma weryfikacji poprawnosci
rozkadów wielkosci ziaren otrzymywanych opisana metoda. Alternatywne
(gównie mikroskopowe) metody wyznaczania wielkosci ziaren zawodza
dla obiektów tak maych jak kilka czy kilkadziesiat nanometrów. Brak
w literaturze wskazan co do metod charakteryzacji obiektów o rozmiarach
wiekszych niz skala atomowa (gdzie mamy np. EXAFS) lecz mniejszych
od zdolnosci rozdzielczej metod mikroskopowych. Dyfrakcja rentgenowska
z teoria uwzgledniajaca warunki brzegowe rozpraszania (dystrybucja
ksztatu nanokrysztaów) pozwala na wypenienie tej luki.
W Dodatku A.1 przedstawiono uzupenienie opisanej metody
polegajace na bezposrednim wykorzystaniu parametrów funkcji Pearson7,
otrzymywanych podczas dopasowywania linii dyfrakcyjnych ta wasnie
krzywa w popularnych programach krystalograficznych.
roman pielaszek
2003-01-13
![]() i
i
![]() jej wysokosci (czyli
FW
jej wysokosci (czyli
FW![]() M i
FW
M i
FW![]() M).
Teoretycznie najlepiej mierzyc szerokosci linii tam gdzie róznia sie
najbardziej, czyli blisko wierzchoka i u podstawy linii. Z praktyki
natomiast wiadomo, ze niewiele punktów doswiadczalnych wierzchoka
i problemy z odcieciem ta u podstawy moga powodowac duze bedy pomiarowe
szerokosci linii. Uzyte wartosci
M).
Teoretycznie najlepiej mierzyc szerokosci linii tam gdzie róznia sie
najbardziej, czyli blisko wierzchoka i u podstawy linii. Z praktyki
natomiast wiadomo, ze niewiele punktów doswiadczalnych wierzchoka
i problemy z odcieciem ta u podstawy moga powodowac duze bedy pomiarowe
szerokosci linii. Uzyte wartosci
![]() i
i
![]() stanowia kompromis miedzy teoria a praktyka. Stwierdzono, ze sa one
uzyteczne zarówno dla dyfraktogramów wyliczonych numerycznie jak i
zmierzonych doswiadczalnie.
stanowia kompromis miedzy teoria a praktyka. Stwierdzono, ze sa one
uzyteczne zarówno dla dyfraktogramów wyliczonych numerycznie jak i
zmierzonych doswiadczalnie.
![]() oraz
oraz
![]() wysokosci jej maksimum. Jest to praca identyczna do wykonanej poprzednio,
kiedy otrzymalismy wyrazenie na szerokosc linii w poowie jej wysokosci
(równanie Scherrera). Uzylismy wtedy wspóczynnika h, który
wyraza uamek wysokosci linii i wynosi
wysokosci jej maksimum. Jest to praca identyczna do wykonanej poprzednio,
kiedy otrzymalismy wyrazenie na szerokosc linii w poowie jej wysokosci
(równanie Scherrera). Uzylismy wtedy wspóczynnika h, który
wyraza uamek wysokosci linii i wynosi
![]() . Tym razem
poozymy najpierw
h =
. Tym razem
poozymy najpierw
h = ![]() a potem
h =
a potem
h = ![]() ,
zachowujac wyprowadzenie od (2.57)
do (2.61) bez zadnej zmiany. Numeryczne
rozwiazanie równan (2.61) daje dwie
krzywe x(m) o nieznanej postaci analitycznej, które jednak
mozemy przyblizyc funkcjami cotangens otrzymujac:
,
zachowujac wyprowadzenie od (2.57)
do (2.61) bez zadnej zmiany. Numeryczne
rozwiazanie równan (2.61) daje dwie
krzywe x(m) o nieznanej postaci analitycznej, które jednak
mozemy przyblizyc funkcjami cotangens otrzymujac:
