Równanie i staa Scherrera dla krysztaów w formie graniastosupa

Porównujac wyrazenie na profil linii dyfrakcyjnej (2.28) z poowa wysokosci tej linii (2.29) otrzymujemy:

LP(q) = $${\frac{{1}}{{2}}}$$$${\frac{{R}}{{\sqrt{2\pi }}}}$$

$$\sqrt{{\frac{2}{\pi }}}$$$${\frac{{1-\cos qR}}{{q^{2}R}}}$$ = $${\frac{{1}}{{2}}}$$$${\frac{{R}}{{\sqrt{2\pi }}}}$$

Po prostych przeksztaceniach dostajemy:

$${\frac{{-4+q^{2}R^{2}+4\cos qR}}{{q^{2}R}}}$$ = 0

Podstawiajac x = qR i zaniedbujac mianownik mamy:

(x² - 4) + 4 cos x = 0 (2.30)

Powyzsze równanie jest równaniem przestepnym, którego jedyny nieujemny pierwiastek, x_o, mozna wyznaczyc graficznie

Figure: Graficzne rozwiazanie równania przestepnego (2.30) wyznaczajacego staa Scherrera dla krysztaów w formie graniastosupa. Pierwiastek równania wynosi ok.  2.78311476, zas staa Scherrera K 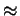$\approx$ 0.88589294.

(rys. 2.18) lub numerycznie z dowolna precyzja. Wynosi on:

x_o $$\approx$$ 2.78311476

Po ponownym podstawieniu x = qR = x_o otrzymujemy zaleznosc poowy szerokosci profilu linii q od wielkosci krysztau R:

q = $${\frac{{x_{o}}}{{R}}}$$

Pamietajac, ze szerokosc poówkowa FWHM = 2q (szerokosc poówkowa to szerokosc obu poówek profilu linii mierzona w poowie jego wysokosci), otrzymujemy równanie Scherrera:

$${\frac{{2x_{o}}}{{R}}} {\frac{{2\pi K}}{{R}}}$$ (2.31)

gdzie K jest staa Scherrera. Z rozwiazania równania przestepnego (2.30) i równania Scherrera (2.31) wynika przyblizona wartosc staej Scherrera dla krysztaów w formie graniastosupa:

K = $${\frac{{2x_{o}}}{{2\pi }}}$$ $$\approx$$ 0.8858929413789046806

Przy wyprowadzaniu równania Scherrera wykorzystano tylko analityczna postac dystrybucji ksztatu odcinka nie korzystajac dalej z zadnych przyblizen, wiec staa Scherrera moze byc wyznaczona ta metoda z dowolnie duza precyzjatypeset@protect @@footnote SF@gobble@opt Tutaj staa Scherrera podano z dokadnoscia 20 cyfr znaczacych z powodów ``ewidencyjnych'': w takiej postaci nadaje sie na unikalny klucz np. przy przeszukiwaniu literaturowych baz danych. Do analizy danych dyfrakcyjnych wystarczaja 3-4 cyfry znaczace. . Obliczona wartosc staej K odpowiada najstarszej podanej przez Scherrera wartosci K = 0.89. Jednak jej stosowalnosc jest ograniczona do krysztaów posiadajacych szczególny ksztat, opisywany przez dystrybucje ksztatu odcinka. O wiele blizsze rzeczywistosci fizycznej jest traktowanie krysztaów jako izotropowych tworów objetosciowych.