Krysztay nie wykazujace wyraznej anizotropii ksztatu moga byc traktowane
jako kuliste. To samo dotyczy krysztaów o ksztatach nieregularnych
lub anizotropowych lecz w losowych kierunkach (np. rozdrobnionych
monokrysztaów kubicznych) oraz wieloscianów foremnych o duzej liczbie
scian (rys. 2.19). We wszystkich wspomnianych
przypadkach dystrybucja ksztatu kuli jest bardzo dobrym lub najlepszym
przyblizeniem dystrybucji ksztatu krysztau.
Figure 2.19:
Typowe ksztaty krysztaów sa dobrze
opisywane dystrybucja ksztatu kuli. a) sciety czworoscian, b) sciety
szescian, c) sciety osmioscian, d) sciety dwunastoscian, e) kryszta
kwarcu, f) kryszta granatu, g) kryszta topazu. Reprodukcje
wieloscianów z [43], modele mineraów wyliczono uzywajac
[44].
|
|
Dystrybucja ksztatu kuli jest znana w postaci analitycznej (2.5):
SD(
r;
R) =


oraz posiada analityczna transformate Fouriera, czyli profil
linii dyfrakcyjnej LP(q) proszku zozonego z identycznych krystalitów
w ksztacie kuli:
LP(q) = FFT(SD(r;R)) = 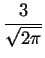 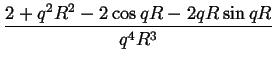 , ,
|
(2.32) |
gdzie R jest srednica krystalitów zas q jest wektorem
rozpraszania. Opisywany przez (2.32) profil linii
(rys. 2.20) zgadza sie z ksztatem maksimów otrzymywanych
przy obliczaniu dyfraktogramów ab initio.
Figure 2.20:
a) Dystrybucja ksztatu kulistego ziarna o
srednicy
50 Å i jej transformata Fouriera
(b) czyli profil linii dyfrakcyjnej.
|
a)
 |
b)
 |
|
Natezenie maksimum profilu otrzymuje sie przez przejscie do granicy
q 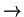 0 w wyrazeniu (2.32):
Podobnie jak poprzednio, przez porównanie (2.32)
i poowy (2.33) mozna wyprowadzic zaleznosc
szerokosci poówkowej profilu linii dyfrakcyjnej od wielkosci krysztau,
czyli równanie Scherrera.
0 w wyrazeniu (2.32):
Podobnie jak poprzednio, przez porównanie (2.32)
i poowy (2.33) mozna wyprowadzic zaleznosc
szerokosci poówkowej profilu linii dyfrakcyjnej od wielkosci krysztau,
czyli równanie Scherrera.
roman pielaszek
2003-01-13
