Porównujac wyrazenie na profil linii dyfrakcyjnej (2.32)
z poowa wysokosci tej linii (2.33) otrzymujemy:
LP(
q) =


Po prostych przeksztaceniach dostajemy:

= 0
Wprowadzajac nieznikajaca zmienna bezwymiarowa x = qR i zaniedbujac
mianownik mamy:
(x2 - 4)2 - 16 2 - cos x - x sin x 2 - cos x - x sin x = 0 = 0
|
(2.34) |
Powyzsze równanie jest przestepne i posiada pojedynczy dodatni pierwiastek,
xo, który mozna znalezc graficznie
Figure:
(a) Graficzne rozwiazanie
równania przestepnego (2.34)
wyznaczajacego staa Scherrera dla krysztaów w ksztacie kuli. Pierwiastek
równania wynosi ok.
3.47665688, zas staa
Scherrera
K 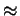 1.10665425. (b) Dla porównania:
staa Scherrera wyznaczona z dziewieciu refleksów
SiC,
GaN i
diamentu obliczonych
ab initio
K = 1.097
1.10665425. (b) Dla porównania:
staa Scherrera wyznaczona z dziewieciu refleksów
SiC,
GaN i
diamentu obliczonych
ab initio
K = 1.097 0.044.
0.044.
|
a)
 b) b)

|
(rys. 2.21a) lub numerycznie
z dowolna skonczona precyzja. Wynosi on:
xo 
3.47665688
Po ponownym podstawieniu
x = qR = xo otrzymujemy zaleznosc poowy
szerokosci profilu linii q od wielkosci krysztau R:
q =

Pamietajac, ze szerokosc poówkowa FWHM = 2q, dostajemy równanie
Scherrera:
FWHM =  = =  , ,
|
(2.35) |
gdzie K jest staa Scherrera. Z rozwiazania równania przestepnego
(2.34) i równania Scherrera
(2.35) wynika przyblizona
wartosc staej Scherrera dla krysztaów w ksztacie kuli:
K =   1.1066542545498348775 1.1066542545498348775
|
(2.36) |
Podobnie jak poprzednio, przy wyprowadzaniu równania Scherrera wykorzystano
tylko analityczna postac dystrybucji ksztatu kuli nie korzystajac
dalej z zadnych przyblizen, wiec staa Scherrera moze byc wyznaczona
ta metoda z dowolnie duza precyzja. Dla porównania obliczono wartosc
staej Scherrera na podstawie kilku najsilniejszych refleksów SiC,
GaN i diamentu (rys. 2.21b)
z ich dyfraktogramów obliczonych ab initio. Z dopasownia zaleznosci
FWHM(R) tych refleksów w skali log-log (rys. 2.21b)
otrzymano zwiazek
FWHM(R) = 6.89153/R. Stad staa Scherrera
K =  = 1.097
= 1.097 0.044.
0.044.
roman pielaszek
2003-01-13

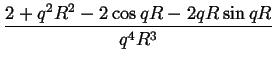 =
= 
 = 0
= 0
 b)
b)
