Najprostsza dystrybucja ksztatu, majaca postac linii prostej (rys. 2.17),
jest dystrybucja ksztatu odcinka (por. rys. 2.6).
Profil linii dyfrakcyjnej, bedacy jej transformata furierowska, odnosi
sie do krysztaów o specyficznym ksztacie: musza one ``dziedziczyc''
z odcinka niektóre jego wasnosci przestrzenne, mianowicie posiadac
os symetrii, wzduz której przekrój krysztau nie zmienia sie na caej
jego dugosci (rys. 2.16), czyli
miec forme graniastosupa. Do tej grupy zaliczaja sie krysztay o
silnej anizotropii ksztatu, czyli silnie wyduzone igy, jak równiez
krysztay pasko sciete, np. pytki. Warunek staosci przekroju speniaja
takze niektóre krysztay izotropowe, np. w ksztacie szescianu. Profil
linii dyfrakcyjnej oparty o dystrybucje ksztatu odcinka odnosi sie
tylko do tych linii bragowskich, których indeks odpowiada wyróznionej
osi staego przekroju.
Figure 2.16:
Krysztay odznaczajace sie
staoscia przekroju (tu: w paszczyznie
X - Y)
na caej swojej dugosci (tu: wzduz osi Z)
posiadaja dystrybucje ksztatu typu odcinka (rys. 2.6a)
ale wyacznie w kierunku swojego wyduzenia. W innych kierunkach dystrybucje
ksztatu maja bardziej skomplikowana postac. Szescian posiada trzy
kierunki ``staego przekroju''.
|
|
Dystrybucja ksztatu odcinka dana jest wzorem:
SD(
r;
R) =


Posiada ona analityczna transformate Fouriera, czyli profil
linii dyfrakcyjnej LP(q), w postaci:
LP(q) = FFT(SD(r;R)) =   , ,
|
(2.28) |
gdzie R jest gruboscia ziarna (odlegoscia miedzy równolegymi
paskimi scianami) zas q jest wektorem rozpraszania. Profil
linii dyfrakcyjnej jest jak widac podobny do gausowskiego (rys. 2.17b),
ale nie jest gausowski.
Figure 2.17:
a) Dystrybucja ksztatu krysztau w formie
graniastosupa o dugosci
50 Å i jej
transformata Fouriera (b) czyli profil linii dyfrakcyjnej.
|
a)
 |
b)
 |
|
Natezenie maksimum profilu otrzymuje sie przez przejscie do granicy
q 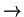 0 w wyrazeniu (2.28):
Przez przyrównanie (2.28) oraz poowy (2.29)
mozna wyprowadzic zaleznosc szerokosci poówkowej profilu linii dyfrakcyjnej
od wielkosci krysztau, czyli równanie Scherrera.
0 w wyrazeniu (2.28):
Przez przyrównanie (2.28) oraz poowy (2.29)
mozna wyprowadzic zaleznosc szerokosci poówkowej profilu linii dyfrakcyjnej
od wielkosci krysztau, czyli równanie Scherrera.
roman pielaszek
2003-01-13
