W paragrafach 2.3.2 i 2.3.4
aby wyprowadzic równanie Scherrera porównywalismy wyrazenie na profil
linii dyfrakcyjnej z poowa jego wysokosci. Teraz postapimy podobnie,
z tym, ze chwilowo zamiast staej
 przed wysokoscia
profilu postawimy wspóczynnik h, któremu dopiero pózniej przypiszemy
wartosc
h =
przed wysokoscia
profilu postawimy wspóczynnik h, któremu dopiero pózniej przypiszemy
wartosc
h =  . To uogólnienie zostanie wykorzystane
w nastepnych paragrafach. O proszku zakadamy, ze jego rozkad wielkosci
ziaren jest postaci (2.43). Dla uproszczenia
równan posugiwac sie bedziemy profilem linii (2.53)
w zmiennych R0 i m, przechodzac na samym koncu do
zmiennych < R > i
. To uogólnienie zostanie wykorzystane
w nastepnych paragrafach. O proszku zakadamy, ze jego rozkad wielkosci
ziaren jest postaci (2.43). Dla uproszczenia
równan posugiwac sie bedziemy profilem linii (2.53)
w zmiennych R0 i m, przechodzac na samym koncu do
zmiennych < R > i 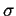 .
.
Porównujac wyrazenie na profil linii dyfrakcyjnej proszku o niezerowej
dyspersji rozkadu wielkosci ziaren (2.53) z uamkiem
wysokosci tej linii h (2.54) otrzymujemy:
LPGSD(q;R0, m) = h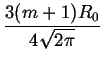 , ,
|
(2.57) |
zas rozwijajac lewa strone:
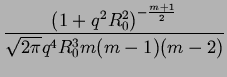 . . |
|
|
|
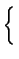 3 3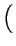 1 + q2R02 1 + q2R02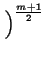 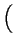 2 + q2R02(m - 1)(m - 2) 2 + q2R02(m - 1)(m - 2)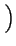 |
|
|
|
-6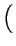 1 + q2R02 1 + q2R02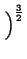 cos cos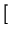 (m - 2)arctan qR0 (m - 2)arctan qR0![$\displaystyle \left.\vphantom{ (m-2)\arctan qR_{0}}\right]$](img312.png) |
|
|
(2.58) |
- ![$\displaystyle \left.\vphantom{ 6qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right.$](img313.png) 6qR0 6qR0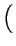 1 + q2R02 1 + q2R02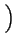 (m - 2)sin (m - 2)sin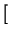 (m - 1)arctan qR0 (m - 1)arctan qR0![$\displaystyle \left.\vphantom{ (m-1)\arctan qR_{0}}\right]$](img316.png) ![$\displaystyle \left.\vphantom{ 6qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right\}$](img317.png) |
= |
h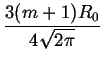 . . |
|
Po przeniesieniu prawej strony równania ze zmienionym znakiem na lewa,
sprowadzeniu do wspólnego mianownika i przegrupowaniu wyrazów dostajemy:
 . . |
|
|
|
![$\displaystyle \left\{\vphantom{ \left( 1+q^{2}R_{0}^{2}\right) ^{\frac{m+1}{2}}...
...-q^{2}R_{0}^{2}\left( hq^{2}R_{0}^{2}m(m+1)-4\right) (m-1)(m-2)\right] }\right.$](img347.png) 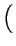 1 + q2R02 1 + q2R02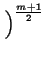  8 - q2R02 8 - q2R02 hq2R02m(m + 1) - 4 hq2R02m(m + 1) - 4 (m - 1)(m - 2) (m - 1)(m - 2)![$\displaystyle \left.\vphantom{ 8-q^{2}R_{0}^{2}\left( hq^{2}R_{0}^{2}m(m+1)-4\right) (m-1)(m-2)}\right]$](img351.png) |
|
|
|
-8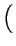 1 + q2R02 1 + q2R02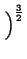 cos cos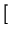 (m - 2)arctan qR0 (m - 2)arctan qR0![$\displaystyle \left.\vphantom{ (m-2)\arctan qR_{0}}\right]$](img312.png) |
|
|
(2.59) |
- ![$\displaystyle \left.\vphantom{ 8qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right.$](img352.png) 8qR0 8qR0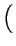 1 + q2R02 1 + q2R02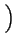 (m - 2)sin (m - 2)sin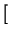 (m - 1)arctan qR0 (m - 1)arctan qR0![$\displaystyle \left.\vphantom{ (m-1)\arctan qR_{0}}\right]$](img316.png) ![$\displaystyle \left.\vphantom{ 8qR_{0}\left( 1+q^{2}R_{0}^{2}\right) (m-2)\sin \left[ (m-1)\arctan qR_{0}\right] }\right\}$](img353.png) |
= |
0 |
|
Korzystajac z faktu, ze symbole q oraz R0 w powyzszym
równaniu zawsze wystepuja parami, podstawimy x = qR0 otrzymujac:
 . . |
|
|
|
![$\displaystyle \left\{\vphantom{ \left( 1+x^{2}\right) ^{\frac{m+1}{2}}\left[ 8-x^{2}\left( hx^{2}m(m+1)-4\right) (m-1)(m-2)\right] }\right.$](img355.png)  1 + x2 1 + x2  8 - x2 8 - x2 hx2m(m + 1) - 4 hx2m(m + 1) - 4 (m - 1)(m - 2) (m - 1)(m - 2)![$\displaystyle \left.\vphantom{ 8-x^{2}\left( hx^{2}m(m+1)-4\right) (m-1)(m-2)}\right]$](img361.png) |
|
|
|
-8 1 + x2 1 + x2 cos cos (m - 2)arctan x (m - 2)arctan x![$\displaystyle \left.\vphantom{ (m-2)\arctan x}\right]$](img364.png) |
|
|
(2.60) |
![$\displaystyle \left.\vphantom{ -8x\left( 1+x^{2}\right) (m-2)\sin \left[ (m-1)\arctan x\right] }\right.$](img365.png) -8x -8x 1 + x2 1 + x2 (m - 2)sin (m - 2)sin (m - 1)arctan x (m - 1)arctan x![$\displaystyle \left.\vphantom{ (m-1)\arctan x}\right]$](img368.png) ![$\displaystyle \left.\vphantom{ -8x\left( 1+x^{2}\right) (m-2)\sin \left[ (m-1)\arctan x\right] }\right\}$](img369.png) |
= |
0 |
|
Po zaniedbaniu mianownika i pierwszego czonu
 1 + x2
1 + x2 ,
który zawsze jest rózny od zera mamy:
,
który zawsze jest rózny od zera mamy:
 1 + x2 1 + x2  8 - x2 8 - x2 hx2m(m + 1) - 4 hx2m(m + 1) - 4 (m - 1)(m - 2) (m - 1)(m - 2)![$\displaystyle \left.\vphantom{ 8-x^{2}\left( hx^{2}m(m+1)-4\right) (m-1)(m-2)}\right]$](img361.png) |
|
|
|
-8 1 + x2 1 + x2 cos cos (m - 2)arctan x (m - 2)arctan x![$\displaystyle \left.\vphantom{ (m-2)\arctan x}\right]$](img364.png) |
|
|
(2.61) |
-8x 1 + x2 1 + x2 (m - 2)sin (m - 2)sin (m - 1)arctan x (m - 1)arctan x![$\displaystyle \left.\vphantom{ (m-1)\arctan x}\right]$](img368.png) |
= |
0 |
|
Powyzsze równanie jest równaniem przestepnym z dwoma niewiadomymi
(h traktujemy jako znane), którego rozwiazaniem jest krzywa
x(m). Równanie to mozna rozwiazac numerycznie traktujac zmienne
m i h jako parametry. Ciag rozwiazan ze wzgledu na parametr
m, przy ustalonym
h =  tworzy monotoniczna
krzywa x(m), pokazana na rys. 2.25
w postaci punktów. Postaci analitycznej tej krzywej niestety nie znamy.
Mozna jednak wykreslic ja dla szerokiego zakresu wartosci m,
który cakowicie pokrywa interesujacy przedzia zmiennosci tego parametrutypeset@protect
@@footnote
SF@gobble@opt
W paragrafie 2.3.6 powiedziano, ze m jest miara
wzglednej szerokosci rozkadu wielkosci ziaren. Praktyka pokazuje,
ze wzgledna szerokosc rozkadu na poziomie
tworzy monotoniczna
krzywa x(m), pokazana na rys. 2.25
w postaci punktów. Postaci analitycznej tej krzywej niestety nie znamy.
Mozna jednak wykreslic ja dla szerokiego zakresu wartosci m,
który cakowicie pokrywa interesujacy przedzia zmiennosci tego parametrutypeset@protect
@@footnote
SF@gobble@opt
W paragrafie 2.3.6 powiedziano, ze m jest miara
wzglednej szerokosci rozkadu wielkosci ziaren. Praktyka pokazuje,
ze wzgledna szerokosc rozkadu na poziomie

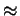 10
(wartosc
m
10
(wartosc
m 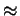 100) wystarcza juz do traktowania proszku
jako bezdyspersyjnego i uprawnia do stosowania modelu opisanego w
2.3.3. Dlatego przy analizie profili linii dyfrakcyjnych
proszków o niezerowej dyspersji rozkadu wielkosci ziaren wystarczy
ograniczyc sie do 0 < m < 100.
. Do tak wykreslonej krzywej mozna nastepnie dopasowac arbitralnie
wybrana funkcje elementarna i traktowac ja dalej jako przyblizenie
nieznanej analitycznie funkcji x(m). Linia ciaga na rys. 2.25
to dopasowanie funkcji cotangens do ciagu rozwiazan równania
(2.61):
100) wystarcza juz do traktowania proszku
jako bezdyspersyjnego i uprawnia do stosowania modelu opisanego w
2.3.3. Dlatego przy analizie profili linii dyfrakcyjnych
proszków o niezerowej dyspersji rozkadu wielkosci ziaren wystarczy
ograniczyc sie do 0 < m < 100.
. Do tak wykreslonej krzywej mozna nastepnie dopasowac arbitralnie
wybrana funkcje elementarna i traktowac ja dalej jako przyblizenie
nieznanej analitycznie funkcji x(m). Linia ciaga na rys. 2.25
to dopasowanie funkcji cotangens do ciagu rozwiazan równania
(2.61):
xh=0.5(m)  0.000585 + 0.004636 . ctg(0.002288 + 0.00135 . m) 0.000585 + 0.004636 . ctg(0.002288 + 0.00135 . m)
|
(2.62) |
Z rys. 2.25 widac, ze jakosc dopasowania
jest bardzo dobra w caym interesujacym nas zakresie wartosci parametru
m i funkcje x(m) mozna traktowac dalej jako znana.
Figure:
Numeryczne rozwiazania równania
przestepnego (2.61) na szerokosc profilu
linii dla ustalonej wartosci parametru h (uamek
wysokosci linii) wyznaczaja zaleznosc
x(m)
(punkty na wykresie), która mozna przyblizyc funkcja typu
x(m) = A + B . ctg(C + D . m)
- linia ciaga. Tutaj: poowa szerokosci poówkowej,
HWHM,
(
h =  ) w funkcji parametru m
rozkadu wielkosci ziaren:
xh=0.5(m) = 0.000585 + 0.004636 . ctg(0.002288 + 0.00135m).
) w funkcji parametru m
rozkadu wielkosci ziaren:
xh=0.5(m) = 0.000585 + 0.004636 . ctg(0.002288 + 0.00135m).
|

|
Pamietajac, ze poprzednio podstawilismy x = qR0 i dysponujac
zaleznoscia x(m) mozna napisac:
q =  , ,
|
(2.63) |
co nie jest jeszcze równaniem Scherrera, gdyz w mianowniku zamiast
sredniego rozmiaru ziarna jest wielkosc R0. Aby otrzymac
równanie Scherrera nalezy pomnozyc (2.63)
obustronnie przez 2, gdyz dopiero FWHM = 2q jest szerokoscia
poówkowa profilu linii:
gdzie:
K = 2  . .
|
(2.65) |
Wyrazenie (2.64) ma postac równania
Scherrera, ale z (2.65), (2.47)
oraz (2.48) wynika, ze staa Scherrera wynosi:
K = K(m) =   = =   = = 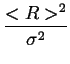  = =  , ,
|
(2.66) |
czyli, ze staa Scherrera dla proszków z niezerowa dyspersja
rozkadu wielkosci ziaren (2.43) jest funkcja
parametrów tego rozkadu, a wiec nie jest to, par excellence,
staa. Dla omawianego rozkadu wielkosci ziaren zaleznosc K(m)
ma nastepujaca postac:
K(m) =  0.000585 + 0.004636 . ctg(0.002288 + 0.00135 . m), 0.000585 + 0.004636 . ctg(0.002288 + 0.00135 . m),
|
(2.67) |
zas pene wyrazenie na szerokosc poówkowa linii dyfrakcyjnej jest
(po podstawieniu
m =  - 1):
- 1):
FWHM( < R > ,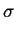 ) = ) =  q q |
= |
K |
|
| |
= |
 0.000585 0.000585 |
|
| |
|
+0.004636 . ctg(0.002288 + 0.00135m) |
|
| |
= |
 0.000585 0.000585 |
(2.68) |
| |
|
+0.004636 . ctg 0.002288 + 0.00135 0.002288 + 0.00135 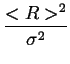 - 1 - 1  |
|
Pamietajac, ze odwrotnosc wzglednej szerokosci rozkadu wielkosci
ziaren (czyli ``monodyspersyjnosc'') to:
 = =  , ,
|
(2.69) |
mozna przedstawic wartosci K w zaleznosci od tego parametru,
czyli funkcje
K( ), co pokazano na rys. 2.26.
Praktyczna minimalna wartosc staej K mozna ocenic
na ok. 0.5, poniewaz odpowiada to
), co pokazano na rys. 2.26.
Praktyczna minimalna wartosc staej K mozna ocenic
na ok. 0.5, poniewaz odpowiada to
 < 1,
czyli dyspersjom
< 1,
czyli dyspersjom 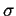 wiekszym od < R >. W tej sytuacji
ziarna wszystkich rozmiarów wystepuja w porównywalnych ilosciach:
mamy mieszanine substancji amorficznej (rozmiar bliski 0 -
pojedyncze molekuy) oraz ziaren o innych wielkosciach wystepujacych
w porównywalnych proporcjach. Wartosc maksymalna
K = 1.0665425
odpowiada proszkowi skadajacemu sie z ziaren o identycznych rozmiarach,
czyli monodyspersyjnemu.
wiekszym od < R >. W tej sytuacji
ziarna wszystkich rozmiarów wystepuja w porównywalnych ilosciach:
mamy mieszanine substancji amorficznej (rozmiar bliski 0 -
pojedyncze molekuy) oraz ziaren o innych wielkosciach wystepujacych
w porównywalnych proporcjach. Wartosc maksymalna
K = 1.0665425
odpowiada proszkowi skadajacemu sie z ziaren o identycznych rozmiarach,
czyli monodyspersyjnemu.
Sens zaleznosci przedstawionej na rys. 2.26
mozna wyrazic nastepujaco: wartosc staej Scherrera zalezy
od wzglednej szerokosci rozkadu wielkosci ziaren. Co wiecej, w
realnie obserwowanych przypadkach zaleznosc ta jest bardzo silna.
Na przykad nanokrystaliczne proszki SiC swiezo po syntezie
(nie poddane zadnej segregacji) maja stosunek
 w zakresie 1÷1.4, co wypada w przedziale silnej zmiennosci
staejtypeset@protect
@@footnote
SF@gobble@opt
Okreslenie ``silna zmiennosc staej'' jest wewnetrznie sprzeczne,
jednak brak odwagi do wypromowania nowego nazewnictwa (np. ``wspóczynnik
Scherrera'') kaze nam pozostac przy istniejacym.
Scherrera. Stosunek ten jest dla materiaów tego samego pochodzenia
zawsze podobny (por. §3.3), niezaleznie od
wielkosci zsyntetyzowanych krystalitów. Zmienia go dopiero intencjonalna
segregacja (frakcjonowanie). Wyobrazmy sobie, ze zsyntetyzowalismy
krystaliczny proszek posiadajacy pewien rozrzut wielkosci ziarna.
Przy pomocy ukadu sit rozdzielamy go na frakcje o coraz precyzyjniej
okreslonych rozmiarach ziaren. Jednoczesnie przy pomocy dyfrakcji
proszkowej i równania Scherrera staramy sie okreslac sredni rozmiar
ziarna w kolejnych frakcjach. Okazuje sie niestety, ze dla kazdej
frakcji powinnismy brac inne stae Scherrera: mniejsze na poczatku
rozdzielania, kiedy proszek jest jeszcze mieszanina ziaren róznych
wielkosci (od, powiedzmy, K = 0.5) a wieksze dla frakcji prawie
monodyspersyjnych (do K = 1.1), gdyz K zalezy wasnie
od szerokosci rozkadu wielkosci ziaren.
w zakresie 1÷1.4, co wypada w przedziale silnej zmiennosci
staejtypeset@protect
@@footnote
SF@gobble@opt
Okreslenie ``silna zmiennosc staej'' jest wewnetrznie sprzeczne,
jednak brak odwagi do wypromowania nowego nazewnictwa (np. ``wspóczynnik
Scherrera'') kaze nam pozostac przy istniejacym.
Scherrera. Stosunek ten jest dla materiaów tego samego pochodzenia
zawsze podobny (por. §3.3), niezaleznie od
wielkosci zsyntetyzowanych krystalitów. Zmienia go dopiero intencjonalna
segregacja (frakcjonowanie). Wyobrazmy sobie, ze zsyntetyzowalismy
krystaliczny proszek posiadajacy pewien rozrzut wielkosci ziarna.
Przy pomocy ukadu sit rozdzielamy go na frakcje o coraz precyzyjniej
okreslonych rozmiarach ziaren. Jednoczesnie przy pomocy dyfrakcji
proszkowej i równania Scherrera staramy sie okreslac sredni rozmiar
ziarna w kolejnych frakcjach. Okazuje sie niestety, ze dla kazdej
frakcji powinnismy brac inne stae Scherrera: mniejsze na poczatku
rozdzielania, kiedy proszek jest jeszcze mieszanina ziaren róznych
wielkosci (od, powiedzmy, K = 0.5) a wieksze dla frakcji prawie
monodyspersyjnych (do K = 1.1), gdyz K zalezy wasnie
od szerokosci rozkadu wielkosci ziaren.
Pod znakiem zapytania stoja próby dokadnego oznaczania wielkosci
ziaren ta metoda w ogóle, skoro do precyzyjnego wyznaczenia wielkosci
ziarna potrzeba dokadnie znac wartosc K, a ta zmienia
sie w funkcji szerokosci rozkadu wielkosci ziaren, którego wasnie
szukamytypeset@protect
@@footnote
SF@gobble@opt
Sredni rozmiar ziarna jest jednym z parametrów rozkadu wielkosci
ziaren.
. Poniewaz K moze zmieniac sie w szerokich granicach, od ok. 0.5
az do 1.1, a wiec nawet dwa razy, taki tez jest mozliwy bad
oznaczenia sredniego rozmiaru krystalitów ta metoda.
Trzeba jednak powiedziec, ze dopóki nie przeszkadza nam bad pomiaru
sredniej wielkosci ziarna na poziomie, przecietnie, kilkudziesieciu
procent, metoda Scherrera jest chyba najlepsza istniejaca, a równiez
najprostsza i niezwykle elegancka. Z przedstawionych przykadów wynika
jednak, ze pomocna byaby mozliwosc wyznaczania z danych dyfrakcyjnych
obu parametrów rozkadu wielkosci ziaren: jego wartosci sredniej i
dyspersji. I to nie tylko dla ograniczenia bedu pomiaru sredniego
rozmiaru ziaren ale gównie dla znalezienia rozrzutu ich wielkosci.
roman pielaszek
2003-01-13
![]() przed wysokoscia
profilu postawimy wspóczynnik h, któremu dopiero pózniej przypiszemy
wartosc
h =
przed wysokoscia
profilu postawimy wspóczynnik h, któremu dopiero pózniej przypiszemy
wartosc
h = ![]() . To uogólnienie zostanie wykorzystane
w nastepnych paragrafach. O proszku zakadamy, ze jego rozkad wielkosci
ziaren jest postaci (2.43). Dla uproszczenia
równan posugiwac sie bedziemy profilem linii (2.53)
w zmiennych R0 i m, przechodzac na samym koncu do
zmiennych < R > i
. To uogólnienie zostanie wykorzystane
w nastepnych paragrafach. O proszku zakadamy, ze jego rozkad wielkosci
ziaren jest postaci (2.43). Dla uproszczenia
równan posugiwac sie bedziemy profilem linii (2.53)
w zmiennych R0 i m, przechodzac na samym koncu do
zmiennych < R > i ![]() .
.
 .
.  .
. .
.  .
.  ,
który zawsze jest rózny od zera mamy:
,
który zawsze jest rózny od zera mamy:


 0.000585
0.000585 0.000585
0.000585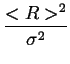 - 1
- 1
![]() w zakresie 1÷1.4, co wypada w przedziale silnej zmiennosci
staejtypeset@protect
@@footnote
SF@gobble@opt
Okreslenie ``silna zmiennosc staej'' jest wewnetrznie sprzeczne,
jednak brak odwagi do wypromowania nowego nazewnictwa (np. ``wspóczynnik
Scherrera'') kaze nam pozostac przy istniejacym.
Scherrera. Stosunek ten jest dla materiaów tego samego pochodzenia
zawsze podobny (por. §3.3), niezaleznie od
wielkosci zsyntetyzowanych krystalitów. Zmienia go dopiero intencjonalna
segregacja (frakcjonowanie). Wyobrazmy sobie, ze zsyntetyzowalismy
krystaliczny proszek posiadajacy pewien rozrzut wielkosci ziarna.
Przy pomocy ukadu sit rozdzielamy go na frakcje o coraz precyzyjniej
okreslonych rozmiarach ziaren. Jednoczesnie przy pomocy dyfrakcji
proszkowej i równania Scherrera staramy sie okreslac sredni rozmiar
ziarna w kolejnych frakcjach. Okazuje sie niestety, ze dla kazdej
frakcji powinnismy brac inne stae Scherrera: mniejsze na poczatku
rozdzielania, kiedy proszek jest jeszcze mieszanina ziaren róznych
wielkosci (od, powiedzmy, K = 0.5) a wieksze dla frakcji prawie
monodyspersyjnych (do K = 1.1), gdyz K zalezy wasnie
od szerokosci rozkadu wielkosci ziaren.
w zakresie 1÷1.4, co wypada w przedziale silnej zmiennosci
staejtypeset@protect
@@footnote
SF@gobble@opt
Okreslenie ``silna zmiennosc staej'' jest wewnetrznie sprzeczne,
jednak brak odwagi do wypromowania nowego nazewnictwa (np. ``wspóczynnik
Scherrera'') kaze nam pozostac przy istniejacym.
Scherrera. Stosunek ten jest dla materiaów tego samego pochodzenia
zawsze podobny (por. §3.3), niezaleznie od
wielkosci zsyntetyzowanych krystalitów. Zmienia go dopiero intencjonalna
segregacja (frakcjonowanie). Wyobrazmy sobie, ze zsyntetyzowalismy
krystaliczny proszek posiadajacy pewien rozrzut wielkosci ziarna.
Przy pomocy ukadu sit rozdzielamy go na frakcje o coraz precyzyjniej
okreslonych rozmiarach ziaren. Jednoczesnie przy pomocy dyfrakcji
proszkowej i równania Scherrera staramy sie okreslac sredni rozmiar
ziarna w kolejnych frakcjach. Okazuje sie niestety, ze dla kazdej
frakcji powinnismy brac inne stae Scherrera: mniejsze na poczatku
rozdzielania, kiedy proszek jest jeszcze mieszanina ziaren róznych
wielkosci (od, powiedzmy, K = 0.5) a wieksze dla frakcji prawie
monodyspersyjnych (do K = 1.1), gdyz K zalezy wasnie
od szerokosci rozkadu wielkosci ziaren.