Postac ROZKADU WIELKOSCI ZIAREN (GSD(r;R), §2.1.4)
nanoproszku zalezy od mechanizmu jego syntezy. Najczesciej przyjmuje
on forme rozkadu log-normalnego (rys. 2.9)
jednomodowego:
lub wielomodowego:
GSDmm(
R) =

 GSD
GSD(
R;
Rmax, j,

),
gdzie sumowanie przebiega po wszystkich modach rozkadu. Aby wprowadzic
niezerowa dyspersje rozmiarów ziaren proszku, nalezy zmodyfikowac
dystrybucje ksztatu ziarna tak, aby opisywaa rozmiar nie jednego,
konkretnego lecz sredniego ziarna proszku. Przejscie od dystrybucji
ksztatu ziarna SD(r;R) do usrednionej dystrybucji ksztatu
ziarna < SD > mozna zapisac, rys. 2.13:
<
SD > (
r;
Rmax,

) =
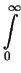 SD
SD(
r;
R)
. GSD(
R;
Rmax,

) d
R
<
SD > (
r;
Rmax,

) =
 SD
SD(
r;
R)
. GSD(
R;
Rmax,

) d
R
 10 . Rmax
10 . Rmax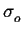 ,
gdzie Rmax jest oczekiwanym maksimum GSD(r;R) zas
,
gdzie Rmax jest oczekiwanym maksimum GSD(r;R) zas
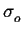 jego dyspersja.
Dystrybucje ksztatu (np. rys. 2.7 i
2.13a) sa wolnozmienne i cakowalne numerycznie w zaniedbywalnym
czasie. Wprowadzenie rozkadu wielkosci ziaren praktycznie nie zwieksza
czasu obliczen opisanego w paragrafie 2.2.2.
Zastosowanie go w obliczeniach dyfrakcji przeprowadza natomiast proszek
monodyspersyjny w polidyspersyjny, który dobrze opisuje rzeczywistosc
fizyczna. Widac to chociazby poprzez porównanie profili dyfrakcyjnych,
rys. 2.13b. Dyfraktogramy obliczone metoda Debye'a
z uwzglednieniem rozkadu wielkosci ziaren stanowia dobre przyblizenie
krzywych mierzonych eksperymentalnie.
jego dyspersja.
Dystrybucje ksztatu (np. rys. 2.7 i
2.13a) sa wolnozmienne i cakowalne numerycznie w zaniedbywalnym
czasie. Wprowadzenie rozkadu wielkosci ziaren praktycznie nie zwieksza
czasu obliczen opisanego w paragrafie 2.2.2.
Zastosowanie go w obliczeniach dyfrakcji przeprowadza natomiast proszek
monodyspersyjny w polidyspersyjny, który dobrze opisuje rzeczywistosc
fizyczna. Widac to chociazby poprzez porównanie profili dyfrakcyjnych,
rys. 2.13b. Dyfraktogramy obliczone metoda Debye'a
z uwzglednieniem rozkadu wielkosci ziaren stanowia dobre przyblizenie
krzywych mierzonych eksperymentalnie.
Figure 2.14:
(a) Profile dyfrakcyjne proszku
SiC
o strukturze regularnej wyliczone przy uzyciu
RDF(r)
i dystrybucji ksztatu sredniego ziarna dla rozkadów wielkosci ziaren
o maksimach od
Rmax = 10Å do
90Å
przy dyspersji
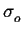 = 0.1. (b) refleks
SiC
(111).
= 0.1. (b) refleks
SiC
(111).
|
a)
 |
b)
 |
|
roman pielaszek
2003-01-13
 exp
exp![$\displaystyle {\frac{{-\left[ \ln \left( R/R_{max}\right) -\sigma _{o}^{2}\right] ^{2}}}{{2\sigma _{o}^{2}}}}$](img147.png)
 SD(r;R) . GSD(R;Rmax,
SD(r;R) . GSD(R;Rmax,