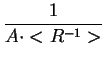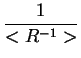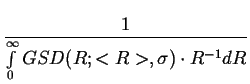Poprzednio pokazalismy, ze dla proszku o jednym wymiarze ziarna istnieje
liniowa relacja pomiedzy rozmiarem ziarna a dugoscia kolumny komórek
elementarnych wyznaczana metoda Warrena-Averbacha, co stanowi podstawe
jej dziaania. Sprawdzimy teraz postac tej samej relacji dla proszków
zozonych z kulistych ziaren z rozrzutem rozmiarów. Procedury Warrena-Averbacha
uzyjemy w odniesieniu do dystrybucji ksztatu usrednionej po rozmiarach
wszystkich krystalitów w proszku < SD >:
| < L > |
= |
- 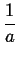 = - = - 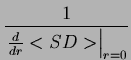 = - = - 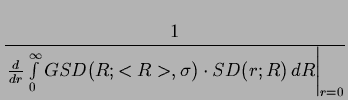 |
|
| |
= |
- 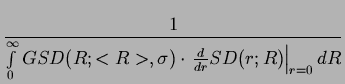 |
(3.8) |
Pochodna dystrybucji ksztatu w zerze ma postac
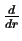 SD(r;R) = -
SD(r;R) = - 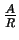 ,
gdzie A jest staa zalezna od ksztatu ziarna, np.
A =
,
gdzie A jest staa zalezna od ksztatu ziarna, np.
A = 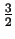 dla krysztaów kulistych czy A = 1 dla krysztaów w formie graniastosupa.
Stad:
dla krysztaów kulistych czy A = 1 dla krysztaów w formie graniastosupa.
Stad:
< L > = 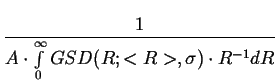 = = 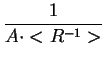
|
(3.9) |
Tak wiec srednia dugosc kolumny komórek elementarnych otrzymywana
z analizy W-A jest proporcjonalna do odwrotnosci momentu statystycznego
rzedu -1 rozkadu wielkosci ziaren < R-1 >. Przeciwnie
do momentu rzedu 1, który jest wartoscia srednia rozkadu < R >
(czyli srednim rozmiarem ziarna), moment < R-1 > nie jest
stowarzyszony z zadna fizycznie interpretowalna wielkoscia. Zaozenie
teorii W-A o liniowej relacji pomiedzy srednia dugoscia kolumny < L >
a srednim rozmiarem ziarna < R > jest wiec spenione tylko w
szczególnym przypadku, o ile zachowana jest równosc:
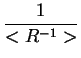 |
= |
< R > |
(3.10) |
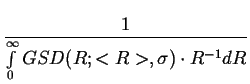 |
= |
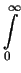 GSD(R; < R > , GSD(R; < R > ,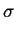 ) . R dR ) . R dR |
(3.11) |
Jest to prawda wtedy i tylko wtedy, gdy:
GSD(R; < R > ,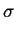 ) = ) = 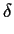 (R - < R > ) (R - < R > ) 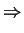 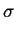 = 0, = 0,
|
(3.12) |
czyli gdy rozkad wielkosci ziaren ma postac delty Dirac'a. Wtedy
caki po obu stronach równania znikaja i otrzymujemy tozsamosc
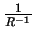 = R.
Innymi sowy metoda Warrena-Averbacha dziaa poprawnie tylko
pod warunkiem braku rozrzutu wielkosci krystalitów w proszku (
= R.
Innymi sowy metoda Warrena-Averbacha dziaa poprawnie tylko
pod warunkiem braku rozrzutu wielkosci krystalitów w proszku (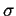 = 0).
Jednak rzeczywiste proszki zawsze posiadaja pewna dyspersje rozmiarów
ziaren. Postaramy sie okreslic wpyw dyspersji na mozliwe bedy na
przykadzie wykadniczo-potegowego i log-normalnego rozkadu wielkosci
ziaren.
= 0).
Jednak rzeczywiste proszki zawsze posiadaja pewna dyspersje rozmiarów
ziaren. Postaramy sie okreslic wpyw dyspersji na mozliwe bedy na
przykadzie wykadniczo-potegowego i log-normalnego rozkadu wielkosci
ziaren.
roman pielaszek
2003-01-13
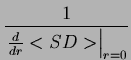 = -
= - 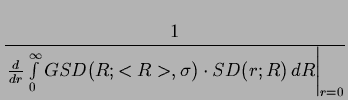
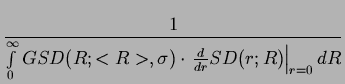
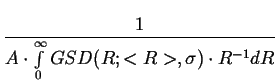 =
=