Wielokrotne obliczanie RDF(r) przypadkowych sekwencji politypowych
moze byc sprowadzone do jednokrotnego obliczenia RDF(r) wszystkich
mozliwych sekwencji. Kazda warstwa w strukturze najgestszego upakowania
wystepuje w jednej z trzech mozliwych pozycji: A, B lub C.
Mozna stworzyc model struktury krystalicznej zawierajacy obsadzone
atomami wszystkie pozycje (A, B i C) w kazdej
warstwie. Tworzy sie tym samym 3-krotnie gestsza siec krystaliczna,
Tab.2.1.
Table 2.1:
Model politypowej struktury krystalicznej
zawierajacej 3 razy wiecej atomów niz w fizycznie istniejacych strukturach
najgestszego upakowania: kazda warstwa ma obsadzone pozycje zarówno
A, B jak i C.
RDF(r)
takiej struktury wyczerpuje wszystkie mozliwe odlegosci miedzyatomowe
(waczajac wiele niefizycznych) dla wszystkich mozliwych sekwencji
politypowych.
|
| Warstwa |
Fizyczna struktura 3C |
Model struktury M-L |
| 1 |
..C..C..C..C..C..C |
ABCABCABCABCABCABC |
| 2 |
.B..B..B..B..B..B. |
ABCABCABCABCABCABC |
| 3 |
A..A..A..A..A..A.. |
ABCABCABCABCABCABC |
| 4 |
..C..C..C..C..C..C |
ABCABCABCABCABCABC |
| 5 |
.B..B..B..B..B..B. |
ABCABCABCABCABCABC |
| 6 |
A..A..A..A..A..A.. |
ABCABCABCABCABCABC |
| 7 |
..C..C..C..C..C..C |
ABCABCABCABCABCABC |
| 8 |
.B..B..B..B..B..B. |
ABCABCABCABCABCABC |
| 9 |
A..A..A..A..A..A.. |
ABCABCABCABCABCABC |
|
Kazdy atom takiej zageszczonej (niefizycznej) sieci moze byc atomem
odniesienia, gdyz jego otoczenie odpowiada sredniemu w caym
krysztale. RDF(r) takiej struktury zawiera wszystkie mozliwe
odlegosci miedzyatomowe które moga sie pojawic przy jakichkolwiek
potencjalnych sekwencjach politypowych.
Aby przeprowadzic taka WIELOWARSTWOWA FUNKCJE ROZKADU RADIALNEGO
(Multi-Layer Radial Distribution Function, MLRDF(r))
w RDF(r) odpowiadajaca pewnemu konkretnemu modelowi nieuporzadkowania,
musza byc zastosowane okreslone reguy wyboru dla odlegosci miedzyatomowych
(niektóre odlegosci w niefizycznej MLRDF(r) sa bardziej prawdopodobne,
niektóre niemozliwe). Te reguy wyboru wyrazone sa przez FUNKCJE
KORELACJI WARSTW (Layer Correlation Function, LCF),
rys. 2.10, i razem z MLRDF(r) prowadza
do RDF(r) usrednionego po sekwencjach politypowych wystepujacych
we wszystkich ziarnach proszku:
< RDF > (r) =   LCFz, l . MLRDFz, l(r) , LCFz, l . MLRDFz, l(r) ,
|
(2.22) |
gdzie N jest liczba warstw w strukturze, l jest pozycja
warstwy (A, B lub C). Dla struktur nieuporzadkowanych
LCF jest zbiezna do staej wartosci
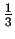 (rys. 2.10b,c).
Dla struktur silnie nieuporzadkowanych (
0.3 < P(h) < 0.7) funkcja
MLRDF(r) nabiera sensu fizycznego juz przy r
(rys. 2.10b,c).
Dla struktur silnie nieuporzadkowanych (
0.3 < P(h) < 0.7) funkcja
MLRDF(r) nabiera sensu fizycznego juz przy r  drugich
sasiadów:
drugich
sasiadów:
|
< RDF > (r) = 0.33(3) . MLRDF(r).
|
(2.23) |
Aby obliczyc dyfraktogram dla modelu proszku posiadajacego jednoczesnie:
- log-normalny rozkad wielkosci ziaren, rys. 2.14
- dowolna konfiguracje bedów uozenia zadana przez P(h), rys. 2.15.
i znajac < RDF > (r) niosaca informacje o srednim otoczeniu atomowym
w caym proszku (usrednionym po lokalnym nieporzadku wszystkich konkretnych
ziaren), mozna uzyc wzoru (2.21) zastepujac
RDF przez < RDF >.
Figure 2.15:
Stadia nieuporzadkowania
SiC
pomiedzy czysta struktura kubiczna i heksagonalna. Parametr heksagonalnosci
zmienia sie od
P(h) = 0 (struktura
3C)
do
P(h) = 1 (struktura
2H).
Profile dyfrakcyjne obliczone ab initio dla
GSD(r;R)
z maksimum w
ro = 140Å i dyspersji
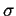 = 0.1.
FUNKCJE KORELACJI WARSTW (
LCF) odpowiadajace
P(h) = 0 (czysta struktura
3C),
P(h) = 0.1 (nieuporzadkowana struktura
3C),
P(h) = 0.9 (nieuporzadkowana struktura
2H)
i
P(h) = 1 (czysta struktura
2H)
sa wykreslone na rys.2.10.
= 0.1.
FUNKCJE KORELACJI WARSTW (
LCF) odpowiadajace
P(h) = 0 (czysta struktura
3C),
P(h) = 0.1 (nieuporzadkowana struktura
3C),
P(h) = 0.9 (nieuporzadkowana struktura
2H)
i
P(h) = 1 (czysta struktura
2H)
sa wykreslone na rys.2.10.
|
|
roman pielaszek
2003-01-13