Rozwazmy zespó statystyczny skadajacy sie z duzej liczby N
nieskonczonych, krysztaów o strukturze najgestszego upakowaniatypeset@protect
@@footnote
SF@gobble@opt
W szczególnosci moga to byc politypowe struktury nieuporzadkowane.
(patrz rys. 1.6). Umiescmy kazdy z nich w osobnym,
kartezjanskim, prawoskretnym ukadzie wspórzednych w nastepujacy
sposób:
- Niech paszczyzny krystaliczne (0001) krysztau beda równolege
do paszczyzny X - Y ukadu.
- Jednostka osi X i Y niech bedzie staa sieci a.
- Jednostka osi Z niech bedzie odlegosc miedzy sasiednimi warstwami
(z bedzie wtedy numerowac warstwy).
- Niech jeden z atomów warstwy z = 0 bedzie umieszczony w punkcie
(0, 0, 0). Warstwe ta nazwijmytypeset@protect
@@footnote
SF@gobble@opt
Umawiamy sie nazywac warstwy przesuniete o
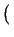 0, 0, z
0, 0, z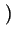
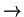 A;
A;
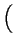
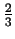 ,
,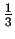 , z
, z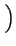
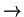 B;
B;
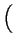
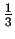 ,
,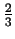 , z
, z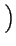
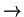 C.
A (tzn. znajdujaca w pozycji A).
C.
A (tzn. znajdujaca w pozycji A).
- Niech jego odpowiednik w warstwie z = 1 bedzietypeset@protect
@@footnote
SF@gobble@opt
Skoro nazwalismy warstwe z = 0 'A', warstwa z = 1
musi byc 'B' lub 'C'. Wymagamy teraz, zeby bya ona
wasnie 'B'. Mozna to wymusic obracajac w razie potrzeby kryszta
wokó osi Z o 180 (co przeprowadza wszystkie warstwy
'C' na 'B' i odwrotnie).
umieszczony w punkcie
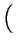
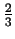 ,
,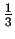 , 1
, 1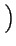 .
Warstwe ta nazwijmy B (tzn. znajdujaca w pozycji B).
.
Warstwe ta nazwijmy B (tzn. znajdujaca w pozycji B).
Opiszmy sekwencje politypowa pojedynczego krysztau ciagiem liter
Sz odpowiadajacych pozycjom warstw, np.
...S-3S-2S-1S0S1S2S3... = ...ABCABCAB....
Warunki 4 i 5 mozemy teraz zapisac nastepujaco:
|
Sz=0 = A, Sz=1 = B
|
(2.11) |
W ten sposób definiujemy pozycje i skretnosc krysztau.
FUNKCJA KORELACJI WARSTW (Layer Correlation
Function, LCF) LCFz, A, LCFz, B, LCFz, C
nazywamy prawdopodobienstwotypeset@protect
@@footnote
SF@gobble@opt
Scisle rzecz biorac jest to prawdopodobienstwo warunkowe przy warunkach
ustalonych w pkt.4 i 5, tzn. ze w z = 0 zawsze znajduje sie warstwa
A, zas w z = 1 zawsze znajduje sie warstwa B.
tego, ze z-ta warstwa krysztau bedzie odpowiednio w pozycji
A, B lub C:
gdzie z jest numerem warstwy; l indeksuje pozycje warstw
(A, B lub C); indeks k numeruje krysztay; 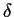 oznacza delte Kroneckera, zas
...Skz(= A, B, C)... opisuje
sekwencje politypowa k-tego krysztau.
oznacza delte Kroneckera, zas
...Skz(= A, B, C)... opisuje
sekwencje politypowa k-tego krysztau.
Dla poszczególnych warstw wyrazenie (2.12) przyjmuje
nastepujace postacie:
Jak widac, w przypadku gdy z = 0 funkcje korelacji warstw redukuja
sie do postaci
LCFA, z=0 = 1,
LCFB, z=0 = 0,
LCFC, z=0 = 0.
FUNKCJA KORELACJI WARSTW opisuje stopien jednowymiarowego
nieuporzadkowania struktury najgestszego upakowania, rys.2.10.
Figure:
FUNKCJA KORELACJI WARSTW
(Layer Correlation Function,
LCF): Prawdopodobienstwo
P(A), P(B) i P(C), ze odlega warstwa bedzie
odpowiednio w pozycji A, B
lub C, gdy warstwa odniesienia
z = 0
jest w pozycji A.
LCF
dla róznych rodzajów nieuporzadkowania: a) czysty polityp
3C:
P(h) = 0; b) nieuporzadkowana struktura
3C:
P(h) = 0.1; c) nieuporzadkowana struktura
2H:
P(h) = 0.9; d) czysty polityp
2H:
P(h) = 1. Dla struktur nieporzadkowanych (b,c)
i odlegych warstw korelacje zanikaja a
LCF
dazy do wartosci sredniej
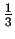 .
.
|
|
Dla struktur uporzadkowanych (periodycznych w kierunku krystalograficznym
c) LCF jest periodyczna i ma okres równy okresowi struktury.
Dla struktur nieuporzadkowanych LCFtypeset@protect
@@footnote
SF@gobble@opt
Na rys. 2.10 skrótowe oznaczenia
P(A), P(B) i P(C)
oznaczaja
P(A) = LCFz, A,
P(B) = LCFz, B i
P(C) = LCFz, C.
jest zbiezna do staej wartosci
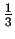 (rys.2.10b,c).
W tym przypadku zbieznosc jest saba (osiagana jest dla
(rys.2.10b,c).
W tym przypadku zbieznosc jest saba (osiagana jest dla
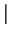 z
z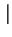
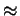 20).
Dla struktur silnie nieuporzadkowanych (gdzie parametr heksagonalnosci
P(h)
20).
Dla struktur silnie nieuporzadkowanych (gdzie parametr heksagonalnosci
P(h) 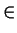 (0.3÷0.7)) LCF zbiega do
(0.3÷0.7)) LCF zbiega do
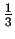 bardzo szybko - juz dla warstw
bardzo szybko - juz dla warstw
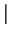 z
z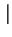 < 5 bedacych
najblizszymi sasiadami warstwy odniesienia z = 0.
< 5 bedacych
najblizszymi sasiadami warstwy odniesienia z = 0.
roman pielaszek
2003-01-13