Nomenclature
    This abstract does not use superscript and subscript for symbols due to a printing reason. Then, some symbols deviate from the conventional nomenclature.
    The presentation uses the conventional nomenclature, e.g., X_M^s*.
________________________
BM  ( YM − YM0 ) / YM0 (-)
c  the growth time such that e1( x, t ) < o1( x, t ) when t < c  (s)
DL, DM   diffusion coefficients for component L, M in liquid solution
e1  the relative discretization error of pL and pM  (-)
e1( x, t )  e1 at x and t  (-)
h  the length of liquid solution in the z direction  (m)
L, M  the most and less affected components by fluid flow
NL  ( XL − XL0 ) / ( XLb − XL0 )  (-)
NL( x, z, t ), NM( x, z, t )  NL and NM at x, z, and t  (-)
NM  ( XM − XM0 ) / ( XMb − XM0 )  (-)
o1  the tolerance of e1  (-)
o1( x, t )  o1 at x and t  (-)
pL, pM  ∂XL / ∂z, ∂XM / ∂z at growth interface  (m⁻¹)
r   ratio of volume per unit atom in the liquid to that in the solid
sqrt( ξ )  the square root of ξ  ( the square root of the unit of ξ )
t  a growth time  (s)
XL, XM  mole fractions of component L, M in liquid phase
XL( x, z, t ), XM( x, z, t )  XL, XM at x, z, and t
XL0, XM0  XL, XM on growth interface when growth has just started
XLb, XMb  XL, XM just before growth
YL, YM  mole fractions of component L, M in solid phase
YL0, YM0  YL, YM when growth has just started
∆zd  the mesh size in the z direction to solve the convection-diffusion equations of solutes  (m)
δL, δM  the boundary layer thicknesses of XL, XM  (m)
κ  a dimensionless parameter characterizing Δzd  (-)

1. Introduction
    We have understood the main behavior of computed results on segregation in numerical simulation of solution growth with fluid flow at the 7th Int. Workshop Model. Cyst. Growth [1]. The present presentation applies that discussion to understand changes in segregation with time. The time dependency had been showed in the 16th Int. Conf. Cryst. Growth [2]. That presentation was comprehensive. The present presentation simplifies the computational models to show the essential matters. The time dependency is discussed more in detail. We understand computed results, watching the fluid flow.
    Conventionally, we cannot grow materials when poorly soluble solutes exist in the liquid solution. For example, we could not grow InGaAlP, which is a material for red LEDs. Aluminum is the poorly soluble solute. On the other hand, GaN grows from sodium solution [3]. In this growth, the fluid flow in the liquid solution plays an important role because it supplies the poorly soluble solute, nitrogen to the growth interface. Thus, it is important to understand the effect of the fluid flow on solution growth. It leads to designing new growth techniques.
    The calculation of segregation is delicate. The boundary layers of solute mole fractions are thin at the initial stage of growth. The mole fractions do not have fixed values on the growth interface. It causes the results to be buried under computational errors. On the other hand, all computed results include errors because the precision of arithmetic is not infinite on the computer, that is, we use finite resources. It is different from the traditional mathematics such as differential calculus. When we compare computed results with the experimental results, it is difficult to separate the error caused by flaws in the model from the error caused by the computation for the model. Moreover, the experimental results itself include errors. Then, we desire to consider the computed results theoretically.

2. Model and computational method
    The x-axis is defined to be in the direction of the main flow. The z-axis is perpendicular to the growth interface. The origin is defined as the center of the growth interface. The computational domain is in the xz plane (Fig. 1a).
    L and M denote components in the liquid solution. XL and XM denote the mole fractions of component L and M in the liquid phase, respectively. YL and YM denote the mole fractions of component L and M in the solid phase, respectively. XL << YL. XM << YM. The liquid solution is supersaturated before the growth. DL and DM denote the diffusion coefficients for component L and M in the liquid solution, respectively. DL > DM. The temperature is uniform and constant during the growth.
    Concretely, we adopt a well-known material to facilitate the verification. We set parameters to approximate the previous experiment [4] (Appendix). The grown material is InGaP. Indium is the solvent of the liquid solution. L = P. M = Ga. YL = 0.5. XLb and XMb denote, respectively, XL and XM just before growth. XLb = 2.8×10⁻². XMb = 9.5×10⁻³. The growth temperature is 1055 K.

2.1 Fluid flow
    The fluid is molten indium and treated as an incompressible Newtonian fluid. The gravity and the change of fluid density dependent on solute mole fractions were neglected. That is, the fluid flow is independent of the situation on solute mole fractions. The basic equations of fluid flow are the conservation of mass and the conservation of momentum. The top of the liquid solution is flat. The slip condition was applied at this boundary. At the other boundaries, the no-slip condition was applied. It was assumed that the velocity perpendicular to the boundaries is zero. It is different from some vapor depositions.
    Before the growth, the liquid solution was stationary and next, a velocity of 20 cm/s was applied on the bottom of the liquid solution for 0.25 s. Finally, this bottom stopped and the growth started. This boundary condition was modeled on the motion of sliding board in liquid phase epitaxy. Such a motion also appears in other techniques.
    The velocities of the fluid flow were computed with SIMPLE [5], which is a computational method in computational fluid dynamics.

2.2 Transport phenomena of solutes
    The diffusion of solutes limits the growth at the growth interface [6]. Convection-diffusion equations of solutes are explicitly solved with the finite difference method.
    δL and δM denote the boundary layer thicknesses of XL and XM, respectively. h denotes the size of liquid solution in the z direction. δM < δL << h. DM / DL = 0.56 [4]. DL = 1.6×10⁻⁸ m²/s [7].
    t denotes a growth time. XL( x, z, t ) and XM( x, z, t ) denote XL and XM at x, z and t, respectively. pL and pM denote ∂XL / ∂z and ∂XM / ∂z at the growth interface, respectively. r denotes the ratio of the volume per unit atom in the liquid to that in the solid. Mass transfer through the growth interface is as follows:
DM ( pM ) / DL / pL
= [ r  (YM ) − XM( x, 0, t )] / [ r ( YL ) − XL( x, 0, t )].
    XL0 and XM0 denote, respectively, XL and XM on the growth interface when the growth has just started. YL0 and YM0 denote, respectively, YL and YM when the growth has just started. At the initial growth, the finite difference cannot express pL and pM. We use the analytic solutions of XL and XM. XL0, XM0 and YM0 were calculated with the method briefly described in Appendix. Ref. 8 provides detailed descriptions on the derivation of them and the meaning of them in the computation.
    The time interval is set so that the results are obtained stably [9]. e1 denotes the relative discretization error of pL and pM. o1 denotes the tolerance of e1. It is estimated from the mass transfer through the growth interface. e1( x, t ) and o1( x, t ) denote e1 and o1 at x and t, respectively. c is defined as the growth time such that e1( x, t ) < o1( x, t ) when t < c. ∆zd denotes the mesh size in the z direction to solve the convection-diffusion equations of solutes. sqrt denotes square root function. It should be determined with the following equations [8] because the computational error does not retain the qualitative properties of the result [10].
1 − sqrt( π ( κ )) erf( 0.5 / sqrt(κ )) < o1.
∆zd = sqrt(( DM ) c / κ ).
Here, κ denotes a dimensionless parameter characterizing Δzd. BM is defined as ( YM − YM0 ) / YM0. In the experiment, BM is of the order of 1×10⁻³. As a result, for c = 0.1 s, the tolerance of BM = 4×10⁻⁵ and o1 = 4×10⁻⁵, ∆zd becomes 20 times finer than the mesh size in the z direction to solve the basic equations of fluid flow. The mesh size in the z direction and time interval to compute XL and XM is much smaller than those to solve the basic equations of the fluid flow. Then, the velocities are interpolated with a cubic spline in the z direction and interpolated linearly in the time domain to obtain the velocities at the grid points for computing XL and XM.
    The mole fractions on the growth interface were implicitly calculated to satisfy the mass transfer and phase diagram.

2.3 Quasi-model and full-model
    Quasi-model [11] was defined as follows:
Mole fractions on the growth interface are calculated only at the origin. These calculated values are substituted for mole fractions at the other points on the growth interface.
    This presentation adds a model and names this model full-model. In this model, the segregation is calculated over the entire growth interface.

2.4 The different conditions from the previous research
     The model and methods are almost same as Ref. 11. The different conditions are as follows. The liquidus line and solidus line are approximated linearly by directly reading the phase diagram of Ref. 6 because we have found the non-linearity and absolute values in phase diagram are not essential matters from the discussions at the previous conferences [1, 2, 7, 10, 11, 12]. Liquidus line: dXM / dXL < −6.5. Solidus line: dYL / dXL = 0, dYM / dXL < −8.


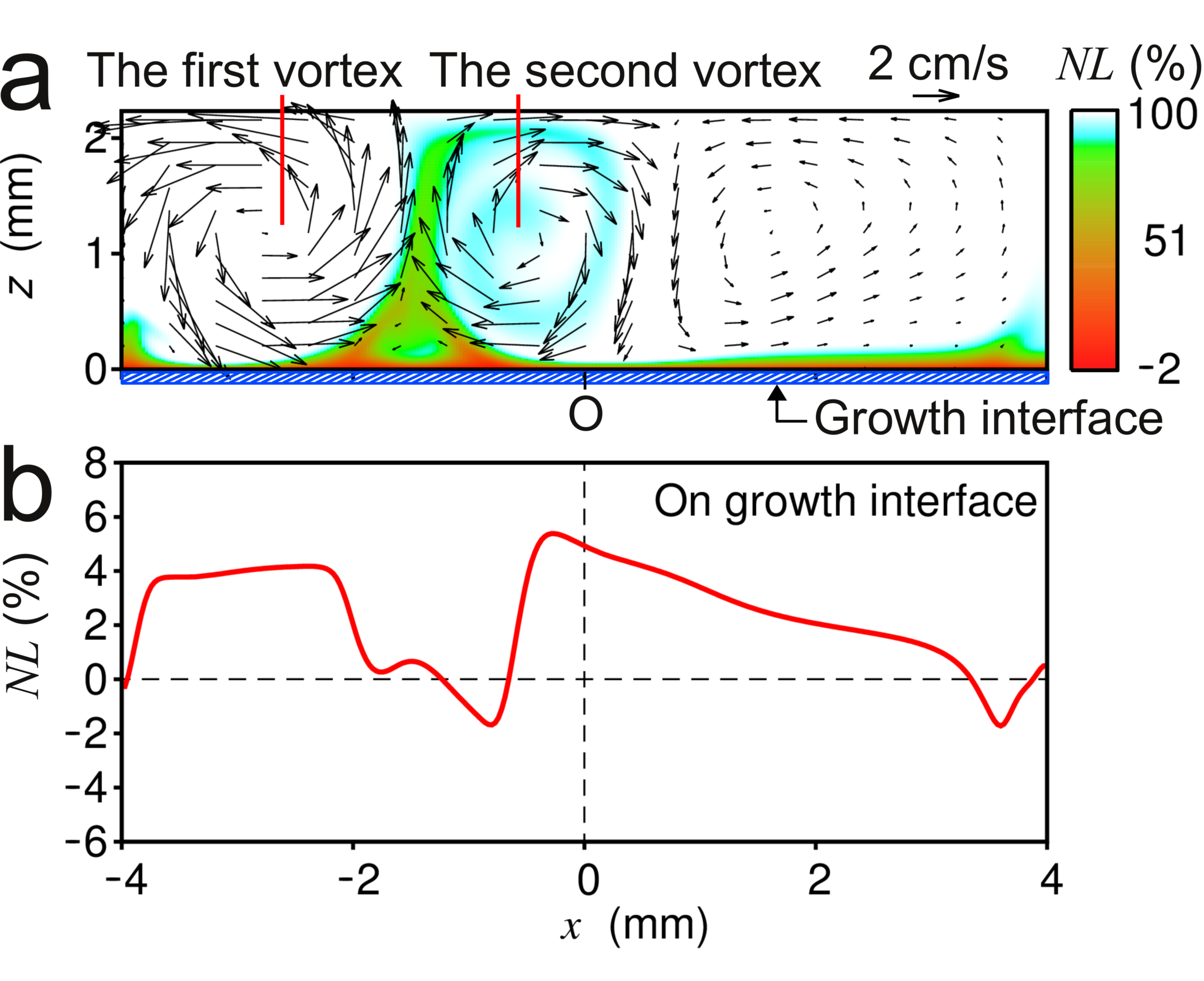
Fig. 1. Computed results at t = 0.35 s in the full-model: (a) flow pattern and normalized mole fraction of component L in the computational domain, (b) normalized mole fraction of component L in the liquid phase on the growth interface.


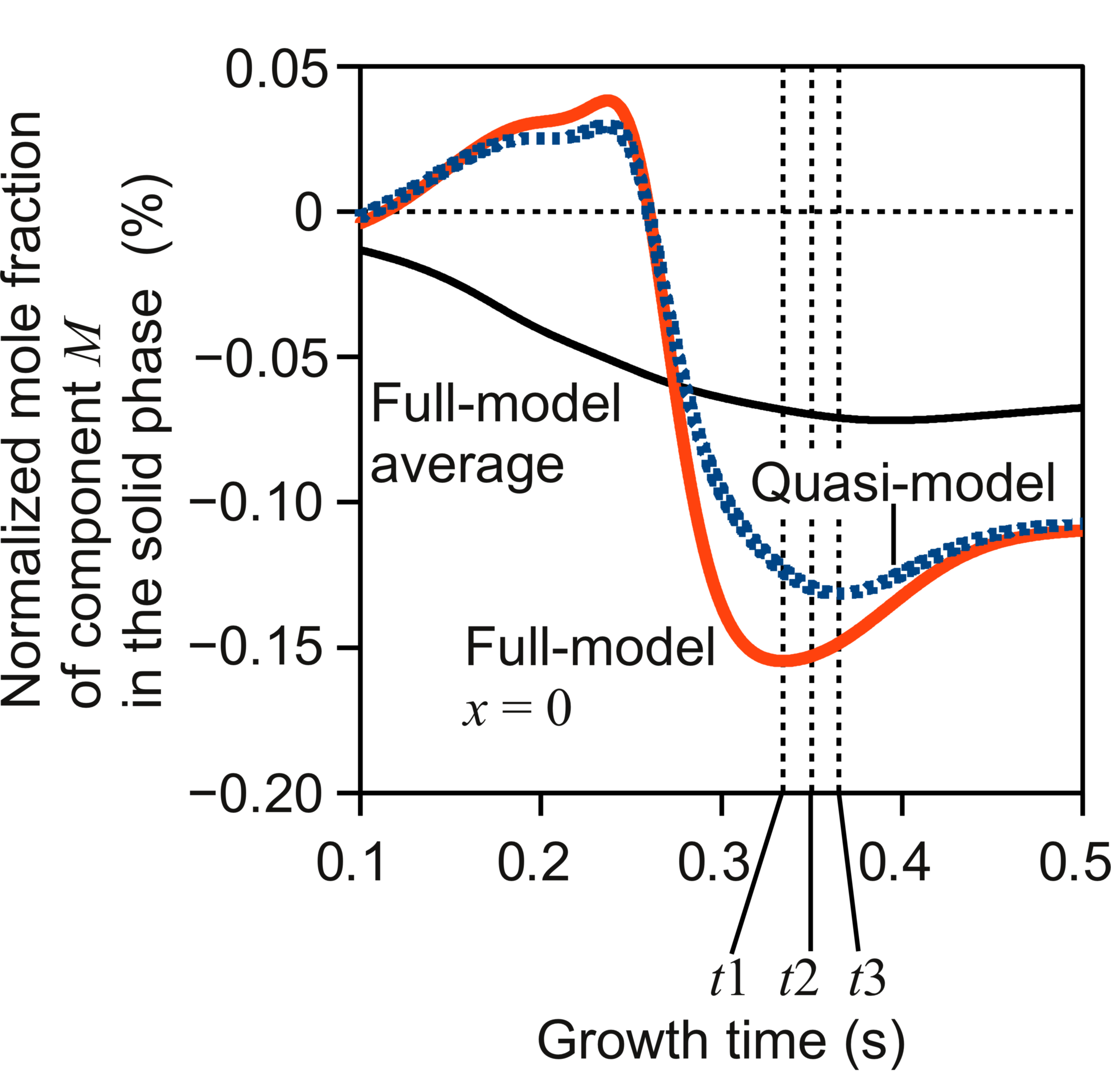
Fig. 2. Growth time vs. normalized mole fraction of component M in the solid phase.

3. Results and discussion
    NL and NM are defined as follows:
NL ≡ ( XL − XL0 ) / ( XLb − XL0 ),
NM ≡ ( XM − XM0 ) / ( XMb − XM0 ).
The normalizations facilitate the understanding of results [1, 12]. The normalized values on the growth interface express the effect of fluid flow because they are zeros for short growth times without fluid flow.
    Fig. 2 shows the time dependency of BM. The dashed curve is a result in the quasi-model. The solid curve similar to the dashed curve is a result at x = 0 in the full-model. The solid curve that shows BM < 0 at all the growth times is the average of BM over the entire growth interface in the full-model. Mainly, BM has lower values than the values without the fluid flow. It is coincident with a previous experiment [4] (Appendix). The variation in the full-model is larger than that in the quasi-model.
    Around t = 0.2 s, BM increases at x = 0, because the fluid flow transports a dilute liquid solution consumed by the growth to the boundary layers of solute mole fractions. This interpretation was reported in the previous conferences [1, 2, 12]. The flow pattern at this time is reported in Ref. 11.
    Around t = 0.3 s, BM decreases at x = 0. The reason was also discussed at the previous conferences. The summary is as follows. The fluid flow transports a liquid solution retaining the initial state to the boundary layers of solute mole fractions. Then, XL increases. XM increases not so much because δM < δL, that is, XM has almost the initial value and increases only slightly. Thus, the fluid flow affects component L most in the solutes. This effect of the fluid flow propagates into the internal region of solute mole fraction boundary layers. Then, on the growth interface, XL increases. XM decreases due to the liquidus line. Therefore, BM decreases.
    t1 and t3 denote the growth times when the values of BM become minimum values in the full-model and quasi-model, respectively. Obviously, t3 is different from t1. The reason is as follows. t2 = 0.35 s. t2 is between t1 and t3. Fig. 1 shows the result of the full-model at t2. Fig. 1a shows the flow pattern and NL. In the shaded region, NL < 0.9. In the white region, NL almost retains the initial state. Fig. 1b shows NL on the growth interface at this time. At x = 0, near the growth interface, the liquid solution flows from the right to the left. In this direction, XL increases near the growth interface. The convection term in this direction has minus values. However, in the quasi-model, XL has the same value over the entire growth interface. Then, the convection term in this direction does not have such minus values. Therefore, BM continues to decrease at this time in the quasi-model. After this time, the momentum of the fluid flow is dissipated by the viscosity. Moreover, the second vortex moves to the left and a block of the fluid flow that has low velocities comes to the center of the growth interface. Then, BM begins to increase in the quasi-model.

4. Conclusion
    We discussed the time dependencies of mole fractions in numerical simulations of solution growth. The temperature was uniform and constant during the growth. The effect of fluid flow was focused on. The computational domain was in a two-dimensional plane. In a quasi-model, mole fractions on the growth interface were calculated only at the center of growth interface. These calculated values were substituted for mole fractions at the other points on the growth interface. In a full-model, the segregation was calculated over the entire growth interface. The mole fraction in the solid phase varied with time. The outline of the variation in the quasi-model was similar to that in the full-model. The average behavior of the mole fraction in the solid phase was coincident with a previous experiment qualitatively. The variation in the full-model was larger than that in the quasi-model. In other words, the quasi-model is more stable than the full-model. It also saves the computational time when the phase diagram has not been calculated yet. Then, it is useful when the computational conditions are unknown. There was a difference of the growth times for a characteristic phenomenon between the quasi-model and full-model. The difference was caused by the approximation specific to the quasi-model, spatial variations of mole fractions on the growth interface and the flow pattern.

Appendix
Initial condition [8]
    XL0, XM0 and YM0 are calculated with the following equation and phase diagram.
sqrt( DM / DL ) ( XMb − XM0 ) / ( XLb − XL0 )
= [ r ( YM ) − XM0 ] / [ r ( YL ) − XL0 ].
————
Previous experiment of solution growth
    Ref. 4 reported an experiment of liquid phase epitaxy. The grown crystal is an InGaP. The solvent is indium. The solutes are phosphorus and gallium. In the present model, L = P and M = Ga. The substrate was separated from the liquid solution before the growth. After the liquid solution was supersaturated, the liquid solution slid to the substrate in order to start the growth. The composition in the solid phase was determined with X-ray diffraction. YM had low values when t < 5 s, compared with the values when t > 5 s.

References
[1] H. Susawa, Ideas to Interpret Computed Results without Floating-Point Arithmetic in Segregation with Fluid Flows, Proc. 7th Int. Workshop Model. Cyst. Growth, The Department of Chemical Engineering, National Taiwan University, (2011) 103-104.
[2] H. Susawa, Numerical simulation of compositional variation in liquid phase epitaxy focusing on the forced convection in the melt, 16th Int. Conf. Cryst. Growth (2010) Session: 01.Fundamental of Crystal Growth (Theory, Simulation, Modeling, Growth Mechanism, Surface and Interfaces) Aug. 11.
[3] F. Kawamura, M. Morishita, M. Tanpo, M. Imade, M. Yoshimura, Y. Kitaoka, Y. Mori, T. Sasaki, J. Cryst. Growth 310 (2008) 3946-3949.
[4] K. Hiramatsu, S. Tanaka, N. Sawaki, I. Akasaki, Analysis of Compositional Variation at Initial Transient Time in LPE Growth of InGaAsP/GaAs System, Jpn. J. Appl. Phys. 24 (1985) 1030–1035.
[5] S.V. Patankar, Numerical Heat Transfer and Fluid Flow, Hemisphere Publishing Corp., Washington, D.C. (1980).
[6] I. Crossley, M.B. Small, The Application of Numerical Methods to Simulate the Liquid Phase Epitaxial Growth of Ga1-xAlxAs from an Unstirred Solution, J. Cryst. Growth 15 (1972) 268–274.
[7] H. Susawa, T. Tsuji, K. Hiramatsu, T. Jimbo, T. Soga, Simulation of InGaP Liquid Phase Epitaxy Including Convection, Theor. Appl. Mech. Jpn. 55 (2006) 279-284.
[8] H. Susawa, T. Tsuji, T. Jimbo, T. Soga, Initial Condition and Calculation Method for the Numerical Simulation of LPE, J. Chem. Eng. Jpn. 40 (2007) 928-938.
[9] P. J. Roache, Computational Fluid Dynamics, Hermosa Publishers Inc., Albuquerque, N.M. (1976).
[10] H. Susawa, Computational Error by Singularity in Segregation from Supersaturated Liquid Solution with Fluid Flows, Proc. 7th Int. Workshop Model. Crtst. Growth, The Department of Chemical Engineering, National Taiwan University, (2011) 39-40.
[11] H. Susawa, T. Tsuji, K. Hiramatsu, T. Jimbo, T. Soga, Simulation of Compositional Variation in Liquid Phase Epitaxy InGaP Using a Two Dimensional Model, Inf. Process. Soc. Jpn. Trans. Math. Model. Appl. 48 No. SIG 2(TOM16) (2007) 147-157.
DOI http://dx.doi.org/10.2197/ipsjdc.3.114.
[12] H. Susawa, Leibniz Institute for Cryst. Growth (IKZ), abstract book of 5th Int. Workshop on Cryst. Growth Technol., Berlin, (2011) 61.

• Legal notice:
  

  Copyright (c) Pielaszek Research, all rights reserved.
  The above materials, including auxiliary resources, are subject to Publisher's copyright and the Author(s) intellectual rights. Without limiting Author(s) rights under respective Copyright Transfer Agreement, no part of the above documents may be reproduced without the express written permission of Pielaszek Research, the Publisher. Express permission from the Author(s) is required to use the above materials for academic purposes, such as lectures or scientific presentations.
  In every case, proper references including Author(s) name(s) and URL of this webpage: https://science24.com/paper/29034 must be provided.

1. The Right and Not Right Solutions for the Model of Growth from Supersaturated Liquid Solution
2. Theorems for Numerical Simulation of Solution Growth with Segregation and Fluid Flow
3. Numerical Calculation Method of Solution Growth and the Main Effect of Fluid Flow