Podsumowanie rozdziau

• Podano szczegóowy opis obliczen ab initio dyfraktogramów polikrysztaów nanometrowych. Na uwage zasuguje fakt, ze przedstawione techniki pozwalaja na cakowicie scise obliczenia dla ziaren wielkosci setek Å, uwzgledniajace rozkad ich wielkosci oraz obecnosc bedów uozenia w strukturach najgestszego upakowania.
• Wykazano, ze wykorzystujac fakt periodycznosci sieci krystalicznej rozpraszajacych drobin (np. nanokrysztaów), wzór Debye'a mozna rozdzielic sie na dwie czesci: strukturalna i mikrostrukturalna. Jest to formalne potwierdzenie intuicyjnego spostrzezenia, ze obserwowany dyfraktogram proszkowy jest splotem poozen (czesc strukturalna) i profili (czesc mikrostrukturalna) linii dyfrakcyjnych.
• Podano analityczne wzory na profil linii dyfrakcyjnej dla trzech mikrostruktur proszków: z ziarnami w formie graniastosupa, kulistymi i ziarnami kulistymi z rozkadem wielkosci ziaren. Wyprowadzone wyrazenia skadaja sie wyacznie z funkcji elementarnych i nie zawieraja zadnych przyblizen.
• Wyprowadzono równania i okreslono stae Scherrera dla znalezionych profili linii dyfrakcyjnych. W przypadku proszku z rozkadem wielkosci ziaren podano zaleznosc wartosci staej Scherrera od wzglednej szerokosci tego rozkadu i okreslono granice stosowalnosci metody Scherrera.
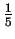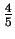• Wobec ograniczonej stosowalnosci (nieliniowosci) równania Scherrera dla proszków polidyspersyjnych, opracowano nowa metode wyznaczania rozkadu wielkosci ziaren. Na podstawie szerokosci linii dyfrakcyjnej mierzonej w dwóch miejscach: w ${\frac{{1}}{{5}}}$ i ${\frac{{4}}{{5}}}$ jej wysokosci pozwala ona na podanie penego rozkadu wielkosci ziaren.
• Podano analityczny wzór na nachylenie krzywej rozpraszania niskokatowego (SAS) w funkcji parametrów rozkadu wielkosci ziaren rozpraszajacego proszku.

Elementy wyróznione pogrubiona czcionka stanowia oryginalny wkad tej pracy i - wedug najlepszej wiedzy autora - nie byy wczesniej publikowane.

Podane w rozdziale 2.3 wzory i metody zostana uzyte w rozdziale 3 do analizy danych doswiadczalnych zebranych dla nanokrysztaów SiC, GaN i diamentu. Jednak ich stosowalnosc nie ogranicza sie do polikrysztaów nanometrowych: sa prawdziwe w ramach zaozen kinematycznej teorii dyfrakcji, czyli nawet dla proszków o ziarnach mikronowych.