


Next: Bibliography
Up: Method of determination of
Previous: Method of determination of
Rozk3ad wielko¶ci ziaren z dopasowania Pearson7
Presented
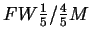 method of GSD determination
is only as precise as measurements of both widths
method of GSD determination
is only as precise as measurements of both widths
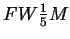 and
and
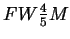 . This precision can be raised by fitting an
analytical curve to the experimental data being evaluated, then measurement
of widths of the analytical (instead of experimental) curve. One of
possible choices could be popular function Pearson7:
. This precision can be raised by fitting an
analytical curve to the experimental data being evaluated, then measurement
of widths of the analytical (instead of experimental) curve. One of
possible choices could be popular function Pearson7:
![\begin{displaymath}
P7(q,a_{0},a_{1},a_{2},a_{3})=\frac{a_{0}}{\left[1+4\left(\f...
...}{a_{2}}\right)^{2}\left(2^{1/a_{3}}-1\right)\right]^{a_{3}}},
\end{displaymath}](img44.png) |
(4) |
where a0 is line intensity, a1 - line position, a2
i a3 are line widths. Putting a0=1 and a1=0 and
comparing expression (4) to 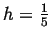 and
and 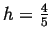 we obtain equation for the width of Pearson7
curve at
we obtain equation for the width of Pearson7
curve at 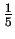 and
and 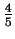 of maximum:
of maximum:
![\begin{displaymath}
\frac{1}{\left[1+4\left(\frac{\Delta q}{a_{2}}\right)^{2}\left(2^{1/a_{3}}-1\right)\right]^{a_{3}}}=h\end{displaymath}](img47.png) |
(5) |
Interesting solutions of above equation are:
Above expressions are functions of parameters a2 and a3,
being immediate result of fitting in a crystallographic software (e.g. PeakFit).
These values
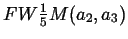 and
and
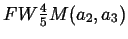 can be placed in equations (3) and we
obtain a recipe how to transform Pearson7 widths to the physical quantities
of <R> and
can be placed in equations (3) and we
obtain a recipe how to transform Pearson7 widths to the physical quantities
of <R> and  , defining Grain Size Distribution:
, defining Grain Size Distribution:



Next: Bibliography
Up: Method of determination of
Previous: Method of determination of
roman pielaszek
2003-03-17
![]() method of GSD determination
is only as precise as measurements of both widths
method of GSD determination
is only as precise as measurements of both widths
![]() and
and
![]() . This precision can be raised by fitting an
analytical curve to the experimental data being evaluated, then measurement
of widths of the analytical (instead of experimental) curve. One of
possible choices could be popular function Pearson7:
. This precision can be raised by fitting an
analytical curve to the experimental data being evaluated, then measurement
of widths of the analytical (instead of experimental) curve. One of
possible choices could be popular function Pearson7:
![\begin{displaymath}
\frac{1}{\left[1+4\left(\frac{\Delta q}{a_{2}}\right)^{2}\left(2^{1/a_{3}}-1\right)\right]^{a_{3}}}=h\end{displaymath}](img47.png)
![\begin{eqnarray*}
A & = & arcctg\left[277069-105723\frac{FW\frac{1}{5}M(a_{2},a_...
...eft[0.002237-2101\cdot A\right]\\
C & = & -0.6515-463695\cdot A
\end{eqnarray*}](img54.png)