Search for content and authors
 

Revision of one-dimensional analytical models of effective segregation coefficient and their application for recovering the crystal growth conditions of space grown GaSb:Te

Alexey E. Voloshin 1,  Anatoly I. Prostomolotov 2,  Nataliya A. Verezub 3,  Tatau Nishinaga 4

1. A.V.Shubnikov Institute of Crystallography The Russian Academy of Sciences, Moscow, Russian Federation
2. Institute for Problems in Mechanics of RAS (IPMECH), Vernadskogo prospect 101, bl. 1, Moscow 119526, Russian Federation
3. Institute for Problems in Mechanics RAS (IPMECH), Vernadskii prospect 101, bl. 1, Moscow 119526, Russian Federation
4. The University of Tokyo, Bunkyo-ku, Tokyo 113-8655, Japan

Abstract

            The well known Burton-Prim-Slichter (BPS) [1] and Ostrogorsky-Muller (OM) [2] 1D analytical models describe in a simple form the dependence of impurity effective segregation coefficient on the crystal growth parameters such as crystal growth rate and melt convective velocity. By this reason they are frequently used for the estimation of actual conditions in realized space crystal growth experiments basing on the impurity concentration profile in the crystal sample. Unfortunately, their adequate trial still was not done. Therefore their validity is not completely clear.

            A careful comparison of both BPS and OM models with the results of 2D numerical simulation carried out by means of widespread Ansys Fluent code [3] has been done in this work for Bridgman growth technique. A wide range of growth cell dimensions and physical parameters (diffusion coefficient, viscosity, crystal growth rate) was tested. For the calculations by BPS model the well known formula for the diffusion layer thickness based on the “flat plate solution” was applied

Here ν is the melt kinematic viscosity, L is the characteristic interface size (growth cell diameter), V∞ is the convective flow velocity beyond the boundary layer, D is the impurity diffusion coefficient in the liquid phase.

            A correspondence between 1D and 2D models was analyzed in terms “mean impurity concentration Cmean” – “maximal Vmax (or mean Vmean) convective velocity”. Both BPS and OM models show a good agreement with 2D calculations (Fig. 1): the misfit did not exceed several percents.

          It was found that from above some cell dimension (L>1.5 cm in the case of material parameters indicated in Fig.1) the agreement is drastically decreases. 2D simulation shows that the melt flow becomes sufficiently two-dimensional and another formula for δ is required. The good result is obtained with

Doc3_5.jpgThe criterion for application of eq. (1) or (2) is discussed.

           

Fig.1 Comparison of 1D and 2D models for the parameters: L=0.6 cm, D=5*10-5 cm2/s, ν=3.75*10-3 cm2/s, k=0.37 (equilibrium segregation coefficient), R=3*10-4 cm/s (crystal growth rate).

            Despite of the good agreement between 1D and 2D calculations, no one of BPS and OM steady state models allow to determine the crystal growth and convective rates simultaneously providing just R/V∞ ratio. We show that study of initial transient regime is required. The expressions for initial transient regime were derived for both BPS and OM models. While C0 is the impurity concentration in the melt beyond the boundary layer, the complete profile of its concentration in the crystal CS is described as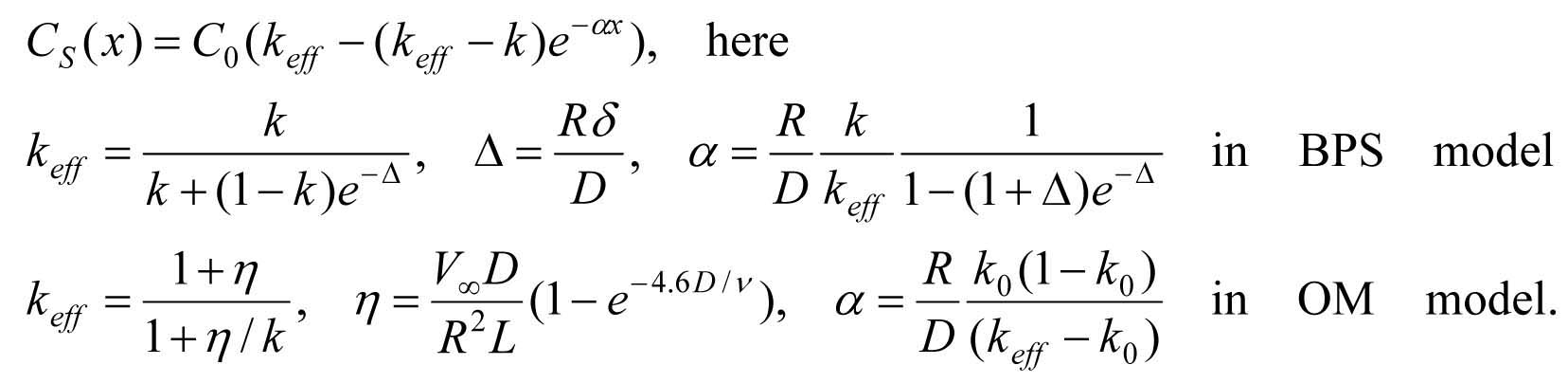           Doc2.jpg             The obtained results were applied to recovering the growth conditions of space grown GaSb:Te, the study of which was reported earlier in [4]. The crystal contains the areas grown by the atomically rough (rounded) interface as well as by the faceted one. The map of Te distribution obtained by quantitative X-ray topography was performed in [3]. It gives the data for recovering the growth conditions in the sample. We succeeded in estimating crystal growth and convective rates, axial and radial thermal gradients, facet supercooling. It was shown that the facet grew by spiral dislocation mechanism. It is demonstrated that even weak temperature variations (~0.1 K) could result in perceptible composition inhomogeneity.

            The possible optimization of space growth conditions based on the carried out estimations is discussed.

             The work is supported by the Russian Foundation for Basic Research (grant No. 12-02-01126).

[1] J. A. Burton, R. C. Prim, W. P. Slichter. J. Chem. Phys., 21 (1953) 1987-1991.

[2] A.G. Ostrogorsky, G. Muller. J. Cryst. Growth, 128 (1993) 207-212.

[3] Ansys CFD // Lisence of IPMECH RAS, No. 659778-23-Aug-2011.

[4] A.E. Voloshin, T. Nishinaga, P. Ge, C. Huo. J. Cryst. Growth, 234 (2002) 12–24.

 

Legal notice
  • Legal notice:

    Copyright (c) Pielaszek Research, all rights reserved.
    The above materials, including auxiliary resources, are subject to Publisher's copyright and the Author(s) intellectual rights. Without limiting Author(s) rights under respective Copyright Transfer Agreement, no part of the above documents may be reproduced without the express written permission of Pielaszek Research, the Publisher. Express permission from the Author(s) is required to use the above materials for academic purposes, such as lectures or scientific presentations.
    In every case, proper references including Author(s) name(s) and URL of this webpage: https://science24.com/paper/29755 must be provided.

 

Related papers
  1. Rubidium-nickel and cesium-nickel sulphates hexahydrates: new crystals for UV band filters
  2. The production of bulk thermoelectric materials based on bismuth and antimony chalcogenide solid solutions by hot extrusion
  3. Simplified numerical approach for estimation of effective segregation coefficient at the melt/crystal interface
  4. The forming of thermoelectric compound by hot extrusion: numerical simulation and microstructure control
  5. The phenomenon of thermal unstability in Czochralski hydrodynamic model: physical and numerical simulation
  6. Peculiarities of the growth and structure formation of new KDP:Al2O3·nH2O composite material
  7. The study of temperature equilibrium of KDP, ADP crystals and solutions from their magnetic treatment

Presentation: Poster at 17th International Conference on Crystal Growth and Epitaxy - ICCGE-17, Topical Session 8, by Alexey E. Voloshin
See On-line Journal of 17th International Conference on Crystal Growth and Epitaxy - ICCGE-17

Submitted: 2013-04-15 17:35
Revised:   2013-04-15 19:31