Rozkďż˝ad dďż˝ugoďż˝ci domen

Rozkad dugosci domen

Ewolucje rozkadu dugosci domen najdogodniej jest przesledzic na przykadzie bardzo dugiej sekwencji czystego politypu 2H, rys. 3.18.

SPL 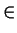$\in$ (0, 0.001) W poczatkowej fazie procesu operator G^-1 dzieli kazda duga wyjsciowa domene 2H na dwie mniejsze (wciaz duze), tworzac jedna izolowana warstwe h (wzrost liczebnosci domen o dugosci 1) i dwie warstwy c.
SPL 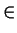$\in$ (0.001, 0.01) W pewnym momencie gwatownie wzrasta prawdopodobienstwo znalezienia krótkiejtypeset@protect @@footnote SF@gobble@opt Krótkiej w porównaniu do dugosci domeny wyjsciowej, tj. dugosci rzedu kilkudziesieciu warstw. domeny heksagonalnej i to praktycznie niezaleznie od jej dugosci. Nieco bardziej prawdopodobne sa domeny najkrótszetypeset@protect @@footnote SF@gobble@opt Zwaszcza w przypadku nanokrysztaów; dokadniejsza dyskusja dalej. . Kryszta osiaga przejsciowy stan nieuporzadkowania, w którym rozkad dugosci domen jest ``biay'' (prawdopodobienstwo znalezienia kazdej dugosci jest podobne).
SPL 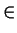$\in$ (0.01, 1) W dalszym ciagu nastepuje rozbicie domen o bardzo zróznicowanej dugosci na krótsze, o podobnych dugosciach. Jednoczesnie operator G^-1 tworzy przy kazdym podziale domeny jedna izolowana warstwe h, ich liczba jest wiec niepomiernie wieksza od domen o wiekszych dugosciach, rys. 3.18b. Przy tej okazji anomalnie wzrasta tez liczba domen o dugosci 3, z racji wasnosci operatora G. Kolejna mozliwa konwersja jest ``doklejenie'' wedrujacych domen 'hh' do powstajacych w duzych ilosciach domen o dugosciach 1 i 3. Zwieksza to prawdopodobienstwo powstania domen 3 i 5 (maksima na rys. 3.18b). Dokonuje sie inwersja obsadzen domen o dugosciach 2 - 3, 4 - 5, itd. na korzysc tych nieparzystych.
SPL 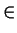$\in$ (0.1, 10) Równolegle operacje P i P^-1 ``rozprowadzaja'' nierównowagowe domeny o nieparzystych dugosciach. W ten sposób równolegle do podziau domen duzszych na krótsze nastepuje konwersja nadreprezentowanych najkrótszych domen w krysztale. Maksima z rys. 3.18b zanikaja.

SPL > 10 Nastepuje uformowanie ostatecznego rozkadu wielkosci domen charakterystycznego dla krysztau cakowicie nieuporzadkowanego.

Figure 3.18: ROZKAD DUGOSCI DOMEN ( DS, pozioma os liniowa) heksagonalnych w trakcie wprowadzania bedów uozenia do krystalitu o strukturze 2H i dugosci 1000000 warstw. Zaawansowanie procesu tworzenia nieporzadku wyrazone jest w przesunieciach na warstwe (Shifts Per Layer, SPL, pozioma os logarytmiczna), a jego kierunek zaznaczono strzaka. Liczba domen (os pionowa) zostaa unormowana do liczby domen w krystalicie. W skali logarytmicznej (a) widac faze procesu (``kana''), w której spektrum dugosci domen jest biae. W skali liniowej (b) widac maksima rozkadu dla domen o dugosciach nieparzystych ( 1, 3, 5). W ostatniej fazie procesu ( SPL > 100) domeny buduja wykadniczy rozkad dugosci - stan cakowitego nieuporzadkowania.

a) $\resizebox*{!}{0.4\textheight}{\includegraphics{eps/hp-GaN/DS-100/rain-AB-1000000-1000-0.1.hblocks.eps}}$ $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/hp-GaN/kierunek_procesu.eps}}$

b) $\resizebox*{!}{0.4\textheight}{\includegraphics{eps/hp-GaN/DS-100/rain-AB-1000000-1000-0.1.hblocks-zoom.eps}}$ $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/hp-GaN/kierunek_procesu.eps}}$

Proces wprowadzania bedów uozenia do innych politypów (4H, 6H, 8H) przebiega podobnie (rys. 3.19) z tym zastrzezeniem, ze bardzo dugie domeny heksagonalne nie istnieja w nich od samego poczatku, wiec przedmiotem dzielenia sa raczej odpowiednie, dugie domeny 4H, 6H i 8H. Zachowuja natomiast waznosc uwagi na temat konwersji nadreprezentowanych najkrótszych domen heksagonalnych i tworzenia ostatecznego rozkadu domen struktury nieuporzadkowanej. Proces rozporzadkowywania struktury 3C jest w ramach prezentowanego modelu cakowicie nieefektywny (rys. 3.19-3C). Mozna mówic o cakowitej rezystywnosci dugich domen 3C na wprowadzanie bedów uozenia opisywana metoda.

Równolegle do rozporzadkowywania domen heksagonalnych nastepuje tworzenie (struktura 2H) lub przeksztacenie (struktury 4H, 6H, 8H) rozkadu wielkosci domen 3C, rys. 3.19, kolumna II. W przypadku struktury 2H kazdy akt podziau domeny przy pomocy operatora G^-1 tworzy dwie domeny 3C o dugosci 1 (warstwy typu c). Tak wiec od samego poczatku procesu nastepuje przyrost ich liczby. W innych politypach domeny 3C wystepuja natywnie, np. w 4H maja one dugosc 1, i nastepuje tylko ich konwersja do innych dugosci w okolicznosciach podobnych do opisanych poprzednio dla domen heksagonalnych.

Pod koniec procesu rozporzadkowywania (SPL > 10) tworzy sie koncowy rozkad wielkosci domen 3C odpowiadajacy strukturze cakowicie nieuporzadkowanej, identyczny z rozkadem domen 2H.

Figure 3.19: Rozkad dugosci domen (Domain Size, DS, pozioma os liniowa) typu 2H (lewa kolumna) i 3C (prawa kolumna) podczas procesu wprowadzania bedów uozenia do czystych politypów 2H, 4H i 3C (kolejne wiersze). Wzrastajacej liczbie przesuniec na warstwe (Shift Per Layer, SPL, pozioma os logarytmiczna) towarzyszy ewolucja rozkadu wielkosci domen az do stanu odpowiadajacego cakowitemu nieuporzadkowaniu (przy SPL $\simeq$ 100). Wyjatek stanowi struktura 3C.

	Rozkad dugosci domen typu 2H	Rozkad dugosci domen typu 3C
2H	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-AB-1000000-1000-0.1.hblocks.eps}}$	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-AB-1000000-1000-0.1.cblocks.eps}}$
4H	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-ABCB-1000000-1000-0.1.hblocks.eps}}$	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-ABCB-1000000-1000-0.1.cblocks.eps}}$
3C	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-ABC-1000000-1000-0.1.hblocks.eps}}$	$\resizebox*{0.45\columnwidth}{!}{\includegraphics{eps/hp-GaN/DS-25/rain-ABC-1000000-1000-0.1.cblocks.eps}}$

roman pielaszek 2003-01-13