W 1950 roku Warren i Averbach przedstawili metode wyznaczania sredniego
rozmiaru krystalitów oraz rozkadu ich wielkosci na podstawie ksztatu
maksimów dyfrakcyjnych [48]. Istota tej metody jest nastepujaca:
wybrane maksimum dyfrakcyjne typu (00l ), po niezbednych korektach
(odjecie ta, korekty na poszerzenie instrumentalne, itp.) rozwija
sie w szereg cosinusów w zakresie obejmujacym oba jego ramiona do
miejsc, gdzie natezenie znika, rys. 3.1. Poczatek
ukadu wspórzednych oraz wierzchoek maksimum umieszcza sie w srodku
tego zakresu (rys. 3.1b). Wspóczynniki rozwiniecia
An dane sa przez:
 r
r =

,
gdzie Ik jest ciagiem 2N + 1 punktów pomiarowych tworzacych
badany refleks w funkcji wektora rozpraszania q (I0
jest natezeniem w maksimum linii, rys. 3.1b);
 q jest cakowita szerokoscia analizowanego refleksu;
n .
q jest cakowita szerokoscia analizowanego refleksu;
n .  r okresla odlegosc w przestrzeni prostej odpowiadajaca
wspóczynnikowi An. Otrzymane z rozwiniecia (3.1)
wartosci wspóczynników An ukadaja sie na szybko malejacej
krzywej (rys. 3.1c). Wedug [40] jej
poczatkowe nachylenie ekstrapolowane az do przeciecia z osia X
wyznacza srednia dugosc < L > kolumn zozonych z komórek elementarnych
krysztau uozonych jedna za druga (rys. 3.2a)
w kierunku (00l ). Srednia < L > jest srednia wazona, której
waga jest równa objetosci kolumny, gdyz natezenie promieniowania jest
proporcjonalne do objetosci materiau rozpraszajacego. Wielkosc < L >
opisuje dugosc kolumny komórek elementarnych (a nie liczbe
komórek elementarnych) i jest liczona w Å.
r okresla odlegosc w przestrzeni prostej odpowiadajaca
wspóczynnikowi An. Otrzymane z rozwiniecia (3.1)
wartosci wspóczynników An ukadaja sie na szybko malejacej
krzywej (rys. 3.1c). Wedug [40] jej
poczatkowe nachylenie ekstrapolowane az do przeciecia z osia X
wyznacza srednia dugosc < L > kolumn zozonych z komórek elementarnych
krysztau uozonych jedna za druga (rys. 3.2a)
w kierunku (00l ). Srednia < L > jest srednia wazona, której
waga jest równa objetosci kolumny, gdyz natezenie promieniowania jest
proporcjonalne do objetosci materiau rozpraszajacego. Wielkosc < L >
opisuje dugosc kolumny komórek elementarnych (a nie liczbe
komórek elementarnych) i jest liczona w Å.
Figure 3.1:
Analiza wielkosci krystalitów metoda Warrena-Averbacha.
a) Obliczony ab initio dyfraktogram (ziarno
SiC
o srednicy
100Å bez dyspersji rozmiaru).
b) Skorygowany profil linii dyfrakcyjnej
SiC(022)
przedstawiony w funkcji odlegosci od srodka linii,
dq.
c) Wspóczynniki szeregu cosinusów,
An
(kropkowana krzywa), powstaego z rozwiniecia profilu (b) niosa dwie
informacje: srednia dugosc kolumny w krysztale (z ekstrapolacji poczatkowego
nachylenia
An, tutaj:
72.6Å)
oraz rozkad dugosci kolumn (druga pochodna
An,
traktowanego jak funkcja ciaga, wzieta z minusem, tutaj: czerwona
amana linia).
|
a)

b)
 |
c)
 |
|
Figure 3.2:
(a) Wielkoscia wyznaczana w
metodzie Warrena-Averbacha jest srednia (wazona) dugosc kolumn
< L >
komórek elementarnych w krysztale. (b) Uamek objetosci zajmowany
przez kolumny o dugosci L w krysztale kulistym
o jednostkowej srednicy.
|
a)
 b)
b)

|
Druga pochodna krzywej tworzonej przez wspóczynniki rozwiniecia
An jest rozkadem dugosci kolumn komórek elementarnych
(CLD(L), Column Length Distribution), równiez z waga
proporcjonalna do objetosci kazdej kolumny:
-   CLD(L), CLD(L),
|
(3.2) |
Rozkad wyraza wiec uamek objetosci krysztau przypadajacy
na kolumny o róznych dugosciach, a nie liczbe kolumn (rys. 3.2b).
Wedug [4, str.273-275] metode Warrena-Averbacha stosowana
poczatkowo do refleksów z grupy (00l ) mozna uzywac dla dowolnego
refleksu dyfraktogramu proszkowego. Zarówno rozkad dugosci kolumn
komórek elementarnych jak i jego wartosc srednia < L > odnosi
sie zawsze do konkretnego kierunku krystalograficznego, zdefiniowanego
przez indeks refleksu (hkl ), którego dotyczy analiza. Profil
(szerokosc) linii (hkl ) odnosi sie wiec do rozmiaru (szerokosci)
krysztau w kierunku [hkl] w przestrzeni prostej. ``Kierunkowosc''
metody W-A powoduje, ze zastosowana do róznych refleksów krysztaów
o silnej anizotropii ksztatu daje rózne wyniki dla kazdego z kierunków.
Na rys. 3.1 przedstawiono przykad analizy
Warrena-Averbacha przeprowadzonej na podstawie dyfraktogramu ``idealnego''
ziarna w ksztacie kuli o srednicy 100Å, bez dyspersji
rozmiaru, obliczonego numerycznie (ab initio), nie zawierajacego
z definicji poszerzen, przesuniec lub asymetrii pochodzacych od ukadu
eksperymentalnego. Z porównania ksztatu rozkadu dugosci kolumn
z rys. 3.2b i takiego samego rozkadu
otrzymanego metoda W-A z analizy dyfraktogramu obliczonego ab initio
(rys. 3.1c, czerwona amana linia) widac, ze
maja one zblizony charakter. Wyliczona z analizy W-A srednia dugosc
kolumny w krystalicie < L > dla testowego dyfraktogramu (rys. 3.1)
wynosi 72.6Å. Nie jest to rozmiar ziarna ale srednia dugosc
kolumny komórek elementarnych. Zazwyczaj interesujacy jest jednak
wasnie rozmiar, lecz aby go na podstawie < L > obliczyc trzeba
znac ksztat ziarna. Ksztat krystalitu najczesciej nie jest z góry
znany i czesto przyjmuje sie, ze jest kulisty. W takim wypadku srednia
dugosc kolumny < L > odpowiada wysokosci walca o objetosci równej
objetosci naszego ziarna i podstawie równej wielkiemu kou naszego
ziarna. Trzymajac sie oznaczen, w których R jest rozmiarem,
a wiec tutaj srednica (nie promieniem!) ziarna piszemy:
skad rozmiar ziarna:
R =  < L > < L >
|
(3.4) |
Tak wiec otrzymana z analizy W-A srednia dugosc kolumny nalezy pomnozyc
przez
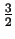 aby uzyskac rozmiar ziarna. W tym testowym
przypadku
R =
aby uzyskac rozmiar ziarna. W tym testowym
przypadku
R = 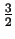 < L > =
< L > = 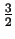 72.6 = 108.9Å.
72.6 = 108.9Å.
Pomimo ze analizowane dane pochodziy z obliczen numerycznych wykonanych
dla proszku bez dyspersji rozmiarów, byy wolne od szumu i próbkowane
z krokiem 0.01Å-1, wynik obarczony jest
10% bedem. Powstaje pytanie, czy rozmiar krystalitu obliczany
ze sredniej dugosci kolumn < L > jest rozmiarem srednim
< R > ziarna w proszku? Zanim odpowiemy na to pytanie, spróbujemy
zinterpretowac sens analizy W-A w swietle informacji zawartych w rozdziale
2.3.
roman pielaszek
2003-01-13

 b)
b)

 =
=