Metoda bezpoďż˝rednia, funkcja korelacji par

Metoda bezposrednia, funkcja korelacji par

Rozwazmy substancje skadajaca sie z L rodzajów atomów, np. Si i C w przypadku SiC, (L = 2). Zbiór wszystkich mozliwych par atomów mozna podzielic na L² podzbiorów par tego samego typutypeset@protect @@footnote SF@gobble@opt Oczywiscie, pary (mn) i (nm), np. (Si - C) i (C - Si) sa równowazne z punktu widzenia wzajemnych odlegosci miedzyatomowych w parze, tak wiec zamiast L² podzbiorów mozna by utworzyc tylko ${\frac{{L(L+1)}}{{2}}}$ . Jednak dla prostoty zostaniemy przy L². , np. (Si - Si), (C - C), (Si - C) i (C - Si). 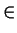Mozemy indeksowac wszystkie typy par jako (mn), gdzie m, n $\in$ (1÷L) opisuje skad pary, np. (11) $\Leftrightarrow$ Si - Si, (22) $\Leftrightarrow$ C - C, (12) $\Leftrightarrow$ Si - C i (21) $\Leftrightarrow$ C - Si.

Teraz równanie Debye'a (2.16) mozna przepisac:

I(q) = $\displaystyle \sum^{{L}}_{{m=1}}$ $\displaystyle \sum^{{L}}_{{n=1}}$ $\displaystyle \sum^{{N_{m}}}_{{i=1}}$ $\displaystyle \sum^{{N_{n}}}_{{j=1}}$ f_mf_n $\displaystyle {\frac{{\sin (q\cdot r_{i,j})}}{{q\cdot r_{i,j}}}}$

I(q) = $\displaystyle {\frac{{1}}{{q}}}$ $\displaystyle \sum^{{L}}_{{m=1}}$ $\displaystyle \sum^{{L}}_{{n=1}}$ f_mf_n $\displaystyle \sum^{{N_{m}}}_{{i=1}}$ $\displaystyle \sum^{{N_{n}}}_{{j=1}}$ $\displaystyle {\frac{{\sin (q\cdot r_{(mn)i,j})}}{{r_{(mn)i,j}}}}$ ,

(2.17)

gdzie pierwsze dwie sumy sa po wszystkich typach par, dwie ostatnie - po wszystkich parach tego samego typu. Poniewaz wielutypeset@protect @@footnote SF@gobble@opt szczególnie w krysztaach parom i, j w wewnetrznej sumie odpowiada ta sama odlegosc miedzyatomowa r_{(mn)i, j}, wygodnie jest skonsolidowac wszystkie odlegosci przez wprowadzenie histogramu odlegosci miedzyatomowych, czyli FUNKCJI KORELACJI PAR (Pair Correlation Function, PCF), rys. 2.11:

PCF_(mn)(r) = 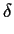$\displaystyle \sum^{{N_{m}}}_{{i=1}}$ $\displaystyle \sum^{{N_{n}}}_{{j=1}}$ $\displaystyle \delta$ (r - r_{(mn)i, j}),

(2.18)

gdzie 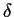$\delta$ jest delta Diraca.

Figure 2.11: a) FUNKCJA KORELACJI PAR obliczona dla (b) sferycznego ziarna SiC, politypu 3C, o srednicy 50Å, 19041 atomów. Pierwsze odlegosci odpowiadaja pierwszym sferom koordynacyjnym, ostatnie - parom atomów lezacych na przeciwlegych powierzchniach ziarna.

a) $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/SiC-50.id.eps}}$

b) $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/sic50.eps}}$

Zmodyfikowane równanie Debye'a (2.17) przyjmuje postac:

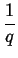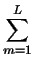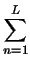I(q) = $\displaystyle {\frac{{1}}{{q}}}$ $\displaystyle \sum^{{L}}_{{m=1}}$ $\displaystyle \sum^{{L}}_{{n=1}}$ f_mf_n $\displaystyle \int\limits^{{R}}_{{0}}$ PCF_(mn)(r) $\displaystyle {\frac{{\sin (q\cdot r)}}{{r}}}$ dr

lub:

I(q) = $\displaystyle {\frac{{1}}{{q}}}$ $\displaystyle \sum^{{L}}_{{m=1}}$ $\displaystyle \sum^{{L}}_{{n=1}}$ f_mf_n $\displaystyle \int\limits^{{R}}_{{0}}$ $\displaystyle {\frac{{PCF_{(mn)}(r)}}{{r}}}$ sin(q^.r)dr,

(2.19)

gdzie R jest wielkoscia (srednica) modelu. Operujac funkcja korelacji par unornowana do jednosci (por. rys. 2.4a i b), nalezy (2.19) dodatkowo pomnozyc przecz cakowita liczbe par atomów w krystalicie. Poniewaz:

$\displaystyle \bigwedge_{{r\notin (0,R)}}^{}$ PCF(r) = 0,

caka w (2.19) jest transformata furierowska, a dokadniej: transformata sinusów funkcji PCF(r)/r. W praktyce uzywa sie szybkiej transformaty Fouriera (Fast Fourier Transform, FFT), odrzucajac jej czesc rzeczywista (cosinusowa):

I(q) = $\displaystyle {\frac{{1}}{{q}}}$ $\displaystyle \sum^{{L}}_{{m=1}}$ $\displaystyle \sum^{{L}}_{{n=1}}$ f_mf_n^.FFT $\displaystyle \left(\vphantom{ \frac{PCF_{(mn)}(r)}{r}}\right.$ $\displaystyle {\frac{{PCF_{(mn)}(r)}}{{r}}}$ $\displaystyle \left.\vphantom{ \frac{PCF_{(mn)}(r)}{r}}\right)$

(2.20)

Korzystajac z (2.20) mozna obliczyc dyfraktogram proszkowy dowolnego klastera atomów bez wzgledu na jego strukture, uporzadkowanie czy skad, zarówno w zakresie rozpraszania niskokatowego (SAS) jak i dyfrakcji bragowskiej, rys. 2.12. Czesc niskokatowa krzywej zawiera charakterystyczne oscylacje o okresie $\Delta$ q = 1/R, gdzie R jest wielkoscia ziarna. Biora sie one z nadreprezentacji odlegosci odpowiadajacych wielkosci ziarna, przy cakowitym braku odlegosci wiekszych i mniejszych. Mamy tu do czynienia ze sztucznym modelem proszku skadajacego sie z ziaren identycznej wielkosci (proszek monodyspersyjny), podczas gdy w rzeczywistosci zawsze mamy do czynienia z dyspersja rozmiarów ziaren (o czym mowa w dalszej czesci).

Figure 2.12: Dyfraktogram proszkowy obliczony dla modelu pokazanego na rys.2.11 ( R = 50Å) przy uzyciu formuy Debye'a. a) Pena krzywa uwzgledniajaca SAS w skali log-log. W zakresie q 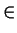$\in$ (0.1÷1.5)Å ^-1 widac interferencje o okresie $\Delta$ q = 1/R = 0.02 spowodowane przez monodyspersyjnosc modelu proszku. b) Czesc bragowska dyfraktogramu

a) $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/sic50-SAS-direct.eps}}$

b) $\resizebox*{!}{0.25\textheight}{\includegraphics{eps/sic50-LAS-direct.eps}}$

Bezposrednie obliczenie dyfraktogramu proszkowego przy pomocy opisanej metody kosztuje $\sim$ R⁶ operacji, gdyz liczba atomów w modelu N $\sim$ R³, wiec obliczenie PCF(r) wymaga $\sim$ N² = $\left(\vphantom{ R^{3}}\right.$ R³ $\left.\vphantom{ R^{3}}\right)^{{2}}_{}$ = R⁶ kroków. PCF(r) mozna obliczyc szybciej uzywajac pojecia FUNKCJI ROZKADU RADIALNEGO RDF(r) i DYSTRYBUCJI KSZTATU.

roman pielaszek 2003-01-13