| Search for content and authors |
Analytical and numerical study of nanoisland spectrum evolution |
| Maxim Nazarenko 1,2, Nickolay V. Sibirev 1,2,3, Maxim Kazansky 1, Vladimir G. Dubrovskii 1,2 |
|
1. St Petersburg Academic University, Khlopina Str 8/3, S.Petersburg 194021, Russian Federation |
| Abstract |
Introduction Classical nucleation-condensation theory is based on the kinetic Zeldovich equation in partial derivatives of the second order for the distribution of nanoparticles over sizes [1-4]. This equation is obtained as a continuous approximation of finite-difference master equations in the monomer limit, where the growth-evaporation rates are related via the detailed balance with the known minimum work of nanoparticle formation [5]. Since the growth equation contains unknown supersaturation of a metastable phase, one should also consider the material balance [2-4]. In an open system with pumping, the supersaturation changes in time due to the monomer consumption by the growing nanoparticles and the material influx into the system [1-3]. Analytical or numerical studies of a particular condensing system therefore requires a solution of two connected equations for the time-dependent size distribution and the supersaturation: the differential Zeldovich equation and the integral equation of material balance [2,3]. Steep exponential dependence of nucleation rate on the supersaturation [1,2] makes the whole system strongly non-linear. The non-linearity of the equations, the fluctuation-induced effects and many other factors make the nucleation-condensation theory rather complex for the analysis. Such analysis is of great importance however in connection with thin films and surface islands [1,4], semiconductor quantum dots (QDs), freestanding nanowires and many other applications. Green function and dispersion increaseBelow we study the case of homogeneous nucleation in the monomer approximation with the growth-evaporation processes (i)+(1)⇔(i+1), where (i) denotes the embryo containing i monomers and (1) is the monomer in a metastable mother phase. The corresponding growth rate Wi+ is assumed to be of quite general form [1-4]: Following Kuni [2], we define invariant size ρ as ρ=i1/m, so that dρ/dt=ζ/τ. А new time-dependent variable z(t) is defined as the most representative invariant nanoparticle size at time t. The Zeldovich equation for the nanoparticle distribution function f(ρ,z) in supercritical region can be written as During the growth stage, Green function g(ρ,z) of the Zeldovich equation (1) can be asymptotically found in the form of Gaussian with z-dependent dispersion ψ(z): 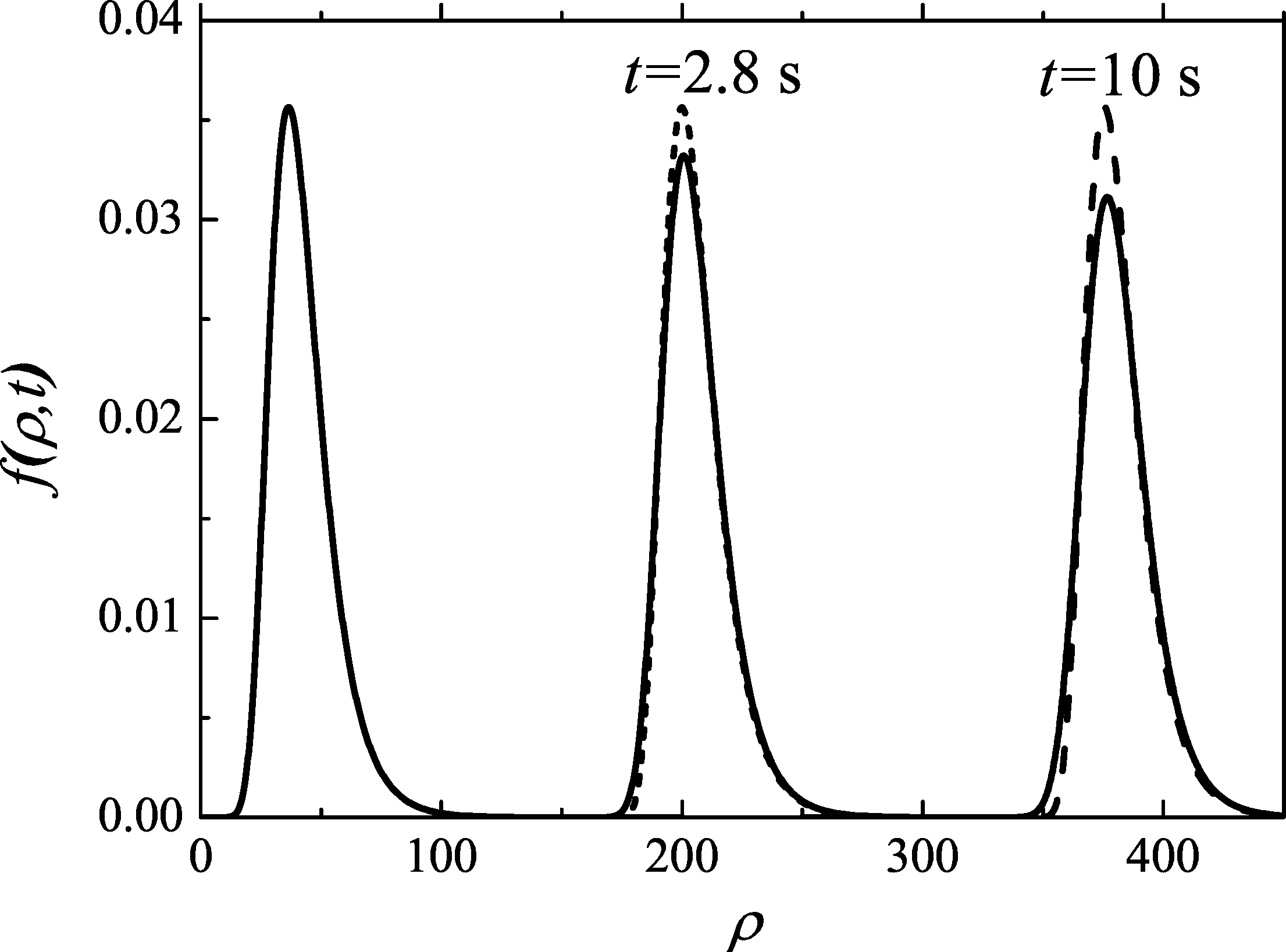 Figure 1. Time evolution of 2D nanoislands size spectrum in m=2 case. Dashed line show time-invariant spectrum. Figure 1. Time evolution of 2D nanoislands size spectrum in m=2 case. Dashed line show time-invariant spectrum.
Direct numerical simulations Numerical simulation allows us to consider critical size, absent in the Zeldovich equation (1). Following Ref. [7] we introduce U as U=(ρ/ρc)m/d, ρc being the critical size and d being the nanoparticle dimension. Assuming (1-U)ln(ζ+1)«1 we can arrive at the following equation for the nanoparticle distribution function By solving equation (2) with the appropriate boundary conditions numerically we are able to compute the spectrum dispersion D. The results are presented in Figure 3. The parameters used correspond to GaAs nanoisland formation. While the simplified analytical approximation and the numerical results agree qualitatively, the subcritical nanoparticles do change the quantitative results.
Ostwald ripening The OR process onsets when the critical size reaches the pre-existing size distribution, and larger embryos start growing at the expense of smaller ones. This effect has a major impact on the size spectrum: the number of particles is no longer conserved and the dispersion increases much faster than at the growth stage. By the very nature of the OR stage, its analysis require one to consider large time intervals, so direct numerical simulation we use above becomes infeasible. Therefore, we apply the explicit scheme of the Crank-Nicolson finite difference method [8] on a regular grid, which allows us to study times up to 106 s. We compare our result to those predicted by Lifshits and Slezov (LS) [9] using the standard LS notation: Conclusions To sum up, we present both analytical and numerical study of nanoparticle size spectrum evolution. The Green function for the second order Zeldovich equation allows us to find size spectrum at the growth stage accounting for the dispersion increase. Direct numerical calculation enable us to consider the critical size influence and to perform an independent check of the previous analytical results. Moreover, a slightly different numerical technique allows us to consider OR stage at times up to 106 s.
Acknowledgments. This work was partially supported by different grants of RFBR. References
|
| Legal notice |
|
| Related papers |
Presentation: Oral at 17th International Conference on Crystal Growth and Epitaxy - ICCGE-17, General Session 1, by Maxim NazarenkoSee On-line Journal of 17th International Conference on Crystal Growth and Epitaxy - ICCGE-17 Submitted: 2013-04-08 12:08 Revised: 2013-07-19 00:01 |